题目内容
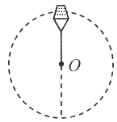
【题目】如图所示，A、B两卫星绕地球运行，运动方向相同，此时两卫星距离最近，其中A是地球同步卫星，轨道半径为r。地球可看成质量均匀分布的球体，其半径为R，自转周期为T。若经过时间t后，A、B第一次相距最远，下列说法正确的有
A. 卫星B的周期为
B. 卫星B的周期
C. 在地球两极，地表重力加速
D. 由题目条件可以求出卫星B的轨道半径
【答案】CD
【解析】
卫星A的运行周期等于地球自转周期T．设卫星B的周期为T′．当卫星卫星B比A多转半周时，A、B第一次相距最远，则有：
，解得：T′=
,故AB错误。对于卫星A，根据万有引力提供向心力，可得：
，可得地球的质量：
；在地球两极，据万有引力等于重力，可得：m′g=G
；联立解得：
，故C正确。根据开普勒第三定律得：
，r、T已知，T′能求出，可知能求出卫星B的轨道半径rB．故D正确。故选CD。
练习册系列答案
相关题目
