题目内容
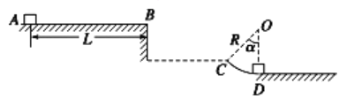
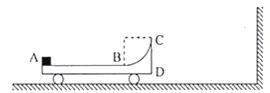
【题目】如图所示,质量M=5kg的小车静止在光滑水平地面上,小车左侧AB部分水平,右侧BC部分为半径R=0.5m的竖直光滑![]() 圆弧面,AB与BC恰好在B点相切,CD为竖直侧壁。质量m=1kg的小滑块以v0=6m/s的初速度从小车左端的A点滑上小车,运动到B点时与小车相对静止一起向前运动,之后小车与右侧竖直墙壁发生碰撞,碰撞前后无能量损失。已知滑块与小车AB段间的动摩擦因数μ=0.5,重力加速度g=10m/s2,求:
圆弧面,AB与BC恰好在B点相切,CD为竖直侧壁。质量m=1kg的小滑块以v0=6m/s的初速度从小车左端的A点滑上小车,运动到B点时与小车相对静止一起向前运动,之后小车与右侧竖直墙壁发生碰撞,碰撞前后无能量损失。已知滑块与小车AB段间的动摩擦因数μ=0.5,重力加速度g=10m/s2,求:
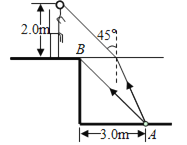
(1)小车与墙壁碰撞前的速度大小;
(2)小车AB段的长度;
(3)试通过计算说明:小车与墙壁碰撞后,滑块能否从C点滑出。
【答案】(1)1m/s;(2)3m;(3)不能。
【解析】
(1)取滑块和小车为研究对象,向右为正方向,则由动量守恒可得
![]()
解得:
![]()
即小车刚与墙壁碰撞时的速度大小为1m/s
(2)从滑块刚滑上小车,到相对静止的过程中,由功能关系可知
![]()
解得:
L=3m
(3)小车与墙壁碰撞后,取向左为正方向,由滑块和小车组成的系统水平方向动量守恒,可得
![]()
解得:
![]()
再由碰后滑块上升过程中,滑块与小车组成的系统机械能守恒可得
![]()
解得
![]()
故不能从C点飞出。

练习册系列答案
相关题目