题目内容
(1)在做“用单摆测定重力加速度”的实验中,用主尺最小分度为1mm,游标上有20个分度的卡尺测量金属球的直径,结果如图甲所示,可以读出此金属球的直径为
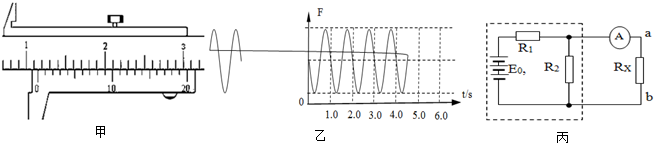
(2)在一些电路中,我们常可以将一部分含电源的未知电路等效成一个不知内阻和电动势的电源.如图所示,电路虚线框内的各元件参数未知,当它的输出端a、b间分别接入不同阻值的电阻Rx时,电流表有不同读数I,则表格中①、②的数值应为①
11.45
11.45
mm.单摆细绳的悬点与拉力传感器相连,将摆球拉开一小角使单摆做简谐运动后,拉力传感器记录了拉力随时间变化的情况,如图乙所示,则该单摆的周期为2
2
s.
(2)在一些电路中,我们常可以将一部分含电源的未知电路等效成一个不知内阻和电动势的电源.如图所示,电路虚线框内的各元件参数未知,当它的输出端a、b间分别接入不同阻值的电阻Rx时,电流表有不同读数I,则表格中①、②的数值应为①
28
28
Ω②0.1
0.1
A,电路虚线框内含电源的未知电路等效成一个电源,则其等效电动势E′和内阻r应为E=12
12
V,r=2
2
Ω.| 1 | 2 | 3 | 4 | |
| Rx/Ω | 10 | 18 | ① | 118 |
| I/A | 1.0 | 0.6 | 0.4 | ② |
分析:(1)游标卡尺的读数等于主尺读数加上游标读数,不需估读.单摆经过平衡位置(最低点)时的速度最大,拉力最大,一个周期摆球两次经过最低点,由图象可以求出单摆周期.
(2)根据闭合电路欧姆定律,利用前两组数据,求出等效电动势和内阻,再由闭合电路欧姆定律求解①、②的数值.
(2)根据闭合电路欧姆定律,利用前两组数据,求出等效电动势和内阻,再由闭合电路欧姆定律求解①、②的数值.
解答:解:(1)由图甲所示游标卡尺可知,主尺示数为11mm,游标尺示数为9×0.05mm=0.45mm,
游标卡尺示数为11mm+0.45mm=11.45mm;
由由图乙所示图象可知,每两次拉力最大值间的时间间隔是2s,单摆周期是2s.
(2)设电路虚线内电源的等效电动势和内阻分别为E和r,根据闭合电路欧姆定律得
E=I1(Rx1+r)…①
E=I2(Rx2+r)…②
将表格中第1组和第2组数据分别代入得:
E=10+r,E=0.6(18+r),
解得:E=12V,r=2Ω
对于第3组数据:I3=0.4A,则有:E=I3(Rx3+r),代入解得:Rx3=28Ω
对于第4组数据:Rx4=118Ω,则有:E=I4(Rx4+r),代入解得:I4=0.1A.
故答案为:(1)11.45,2.(2)28,0.1,12,2.
游标卡尺示数为11mm+0.45mm=11.45mm;
由由图乙所示图象可知,每两次拉力最大值间的时间间隔是2s,单摆周期是2s.
(2)设电路虚线内电源的等效电动势和内阻分别为E和r,根据闭合电路欧姆定律得
E=I1(Rx1+r)…①
E=I2(Rx2+r)…②
将表格中第1组和第2组数据分别代入得:
E=10+r,E=0.6(18+r),
解得:E=12V,r=2Ω
对于第3组数据:I3=0.4A,则有:E=I3(Rx3+r),代入解得:Rx3=28Ω
对于第4组数据:Rx4=118Ω,则有:E=I4(Rx4+r),代入解得:I4=0.1A.
故答案为:(1)11.45,2.(2)28,0.1,12,2.
点评:在第一问中掌握游标卡尺的读数方法,以及知道单摆振动在最低点拉力最大.本题第(2)问中,不要因为虚线框内复杂的电路而干扰,采用等效的思维方法,变成了闭合电路欧姆定律应用问题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 (1)在做“用单摆测定重力加速度”的实验时,用摆长L和周期T计算重力加速度的公式是g=
(1)在做“用单摆测定重力加速度”的实验时,用摆长L和周期T计算重力加速度的公式是g=
 某学生在用单摆测重力加速度的实验时,只量了悬线的长度L当作摆长,而没有加上摆球的半径,让单摆做小角度摆动,测出周期,并用单摆的周期公式,算出了当地的重力加速度.
某学生在用单摆测重力加速度的实验时,只量了悬线的长度L当作摆长,而没有加上摆球的半径,让单摆做小角度摆动,测出周期,并用单摆的周期公式,算出了当地的重力加速度.