题目内容
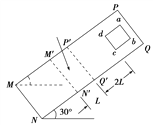
【题目】如图，质量为6m、长为L的薄木板AB放在光滑的平台上，木板B端与台面右边缘齐平．B端上放有质量为3m且可视为质点的滑块C，C与木板之间的动摩擦因数为
．质量为m的小球用长为L的细绳悬挂在平台右边缘正上方的O点，细绳竖直时小球恰好与C接触．现将小球向右拉至细绳水平并由静止释放，小球运动到最低点时细绳恰好断裂．小球与C碰撞后反弹速率为碰前的一半．
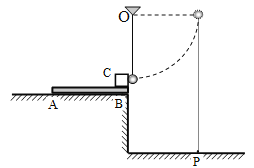
(1)求小球与C碰撞后瞬间滑块C的速度；
(2)若要使小球落在释放点的正下方P点，平台高度应为多大？
(3)通过计算判断C能否从木板上掉下来．
【答案】(1) 
(2) 
(3) 滑块C不会从木板上掉下来．
【解析】 (1)设小球运动到最低点的速率为v0，小球向下摆动过程，由动能定理
① 得
②
小球与滑块C碰撞过程中小球和C系统满足动量守恒，设C碰后速率为v1，向左为正方向，并依题意有
③
得
④
(2)小球碰撞后平抛运动： 
⑤ 水平分位移： 
⑥ 解得： 
⑦
(3) 假设木板足够长，在C与木板相对滑动直到相对静止过程，设两者最终共同速率为v2，
由动量守恒： 
⑧
由能量守恒： 
⑨
联立解得： 
⑩ 由
知，滑块C不会从木板上掉下来．
练习册系列答案
优学名师名题系列答案
相关题目
