Question

如图11所示，一辆质量m=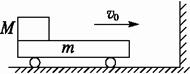2 kg的平板车左端放有质量M=3 kg的小滑块，滑块与平板车之间的动摩擦因数μ=0.4.开始时平板车和滑块共同以v₀=2 m/s的速度在光滑水平面上向右运动，并与竖直墙壁发生碰撞，设碰撞时间极短且碰撞后平板车速度大小保持不变，但方向与原来相反，平板车足够长，以致滑块不会滑到平板车右端.（取g=10 m/s²)求：?

图11

（1）平板车第一次与墙壁碰撞后向左运动的最大距离；?

（2）平板车第二次与墙壁碰撞前瞬间的v；

（3）为使滑块始终不会滑到平板车右端，平板车至少多长？

Answer 1

(1)0.33 m　(2)0.4 m/s　(3)0.833 m?

解析：(1)选小车为研究对象，研究平板车与墙壁碰撞后向左运动的过程，设平板车向左运动的最大距离为s，根据动能定理有?

解得：

(2)选滑块与平板车组成的系统为研究对象，当平板车向左运动到最大距离处时，滑块具有向右的速度，由于摩擦力作用，使板车又向右运动.研究滑块与板车相互作用的过程，根据动量守恒定律得?

Mv₀-mv₀=(M+m)v

解得平板车第二次与墙壁碰撞前瞬间的速度为?

(3)最终车停在墙边，动能全部转化为内能.设滑块相对平板车总位移为l，根据功能关系(摩擦力做功的特点)有?

(M+m)v₀²=μMgl.?

解得：

代入数据得平板车的最短长度为?