题目内容
在轻绳的两端各拴一个小球，一人用手拿着绳上端的小球站在三层楼的阳台上，让小球从静止自由下落，两小球相继落地的时间差为Δt，如果站在四层楼的阳台上，同样放手让小球自由下落，则两小球相继落地时间差将
A.变小 B.变大 C.不变 D.无法判断
【答案】
A
【解析】
试题分析：不论放在三楼阳台释放还是放在四楼阳台释放，两球均做自由落体运动一球落地后，另一球运动的位移相等，根据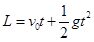
，可求出两球落地的时间差的变化。设细线的长度为L，第一个小球着地后，另一个小球运动的位移为L，在L内运行的时间Δt，即为两球落地的时间差，第一个球着地的速度为另一个小球在位移L内的初速度．高度越高，落地的速度越大，知高度越高，另一个小球在位移L内的初速度越大，根据
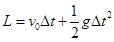，初速度越大，时间越短．所以站在四层楼的阳台上，同样放手让小球自由下落时间越短，故A正确，B、C、D错误。解决本题的关键通过分析得出一球落地后，另一球运动的位移不变，等于绳子的长度；然后根据位移时间关系公式
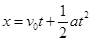，由初速度的大小的变化，判断出两球落地的时间差的变化。
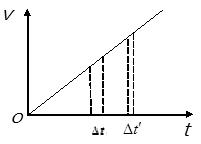
另解：由于两球均做自由落体运动，可画出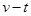
图象，设从三楼阳台释放和四楼阳台释放两小球相继落地时间差分别为Δt和
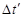，由图可知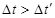
，所以只有B选项正确。
考点：自由落体运动规律的应用
练习册系列答案
相关题目