题目内容
1. 质量为m的木块在拉力作用下在水平地面上做匀速运动,拉力与水平方向夹角为θ,木块与地面间的动摩擦因数μ,试求拉力的大小.
质量为m的木块在拉力作用下在水平地面上做匀速运动,拉力与水平方向夹角为θ,木块与地面间的动摩擦因数μ,试求拉力的大小.
分析 物体匀速运动,说明物体是处于受力平衡状态,由水平和竖直方向的平衡条件分别列方程,加上滑动摩擦力的公式,就能求出拉力的大小.
解答 解:由于物体做匀速运动,对物体受力分析,根据平衡条件,
水平方向有:
Fcosθ=f
竖直方向有:
FN=mg-Fsinθ
滑动摩擦力为:
f=μFN=μ(mg-Fsinθ)
联立解得:F=$\frac{μmg}{cosθ+μsinθ}$
答:拉力的大小为$\frac{μmg}{cosθ+μsinθ}$.
点评 对物体受力分析,由水平和竖直方向和滑动摩擦力的公式分别列方程求解即可.

练习册系列答案
相关题目
11.关于合力和分力的大小关系,下列说法正确的是( )
| A. | 合力一定比每个分力都大 | |
| B. | 合力至少比一个分力大 | |
| C. | 合力可以比任意一个分力都小 | |
| D. | 合力不可能和两个分力的大小都相等 |
9. 如图所示,光滑半球的半径为R,球心为O,固定在水平面上,其上方有一个光滑曲面轨道AB,高度为$\frac{R}{4}$.轨道底端水平并与半球顶端相切,质量为m的小球由A点由静止滑下,最后在水平面上的落点为C(未画出).重力加速度为g,则( )
如图所示,光滑半球的半径为R,球心为O,固定在水平面上,其上方有一个光滑曲面轨道AB,高度为$\frac{R}{4}$.轨道底端水平并与半球顶端相切,质量为m的小球由A点由静止滑下,最后在水平面上的落点为C(未画出).重力加速度为g,则( )
 如图所示,光滑半球的半径为R,球心为O,固定在水平面上,其上方有一个光滑曲面轨道AB,高度为$\frac{R}{4}$.轨道底端水平并与半球顶端相切,质量为m的小球由A点由静止滑下,最后在水平面上的落点为C(未画出).重力加速度为g,则( )
如图所示,光滑半球的半径为R,球心为O,固定在水平面上,其上方有一个光滑曲面轨道AB,高度为$\frac{R}{4}$.轨道底端水平并与半球顶端相切,质量为m的小球由A点由静止滑下,最后在水平面上的落点为C(未画出).重力加速度为g,则( )| A. | 小球将沿半球表面做一段圆周运动后抛至C点 | |
| B. | 小球将从B点开始做平抛运动到达C点 | |
| C. | OC之间的距离为R | |
| D. | 小球到C点时的速率为$\sqrt{\frac{5}{2}gR}$ |
16.物体同时受到同一平面内的三个力的作用,下列几组力的合力不可能为零的是( )
| A. | 3N,4N,8N | B. | 5N,2N,3N | C. | 1N,5N,10N | D. | 10N,10N,10N |
6.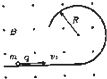 如图所示,一根水平光滑的绝缘直槽轨连接一个竖直放置的半径为R=0.50m的绝缘光滑槽轨.槽轨处在垂直纸面向外的匀强磁场中,磁感应强度B=0.50T.有一个质量m=0.10g,带电量为q=+1.6×10-3C的小球在水平轨道上向右运动.若小球恰好能通过最高点,则下列说法正确的是( )
如图所示,一根水平光滑的绝缘直槽轨连接一个竖直放置的半径为R=0.50m的绝缘光滑槽轨.槽轨处在垂直纸面向外的匀强磁场中,磁感应强度B=0.50T.有一个质量m=0.10g,带电量为q=+1.6×10-3C的小球在水平轨道上向右运动.若小球恰好能通过最高点,则下列说法正确的是( )
 如图所示,一根水平光滑的绝缘直槽轨连接一个竖直放置的半径为R=0.50m的绝缘光滑槽轨.槽轨处在垂直纸面向外的匀强磁场中,磁感应强度B=0.50T.有一个质量m=0.10g,带电量为q=+1.6×10-3C的小球在水平轨道上向右运动.若小球恰好能通过最高点,则下列说法正确的是( )
如图所示,一根水平光滑的绝缘直槽轨连接一个竖直放置的半径为R=0.50m的绝缘光滑槽轨.槽轨处在垂直纸面向外的匀强磁场中,磁感应强度B=0.50T.有一个质量m=0.10g,带电量为q=+1.6×10-3C的小球在水平轨道上向右运动.若小球恰好能通过最高点,则下列说法正确的是( )| A. | 小球在最高点所受的合力为0 | |
| B. | 小球到达最高点时的机械能与小球在水平轨道上的机械能相等 | |
| C. | 如果设小球到达最高点的线速度是v,小球在最高点时式子mg+qvB=$\frac{m{v}^{2}}{R}$成立 | |
| D. | 如果重力加速度取10m/s2,则小球初速度v0=4.6m/s |
13. 如图所示,a、b、c为三个物块,M、N为两个轻弹簧,N弹簧下端固定在水平地面上,上端与c相连接,N弹簧的上端与b相连接,下端与c相连接,R为跨过定滑轮的轻绳,系统静止,则下列说法中正确的有( )
如图所示,a、b、c为三个物块,M、N为两个轻弹簧,N弹簧下端固定在水平地面上,上端与c相连接,N弹簧的上端与b相连接,下端与c相连接,R为跨过定滑轮的轻绳,系统静止,则下列说法中正确的有( )
 如图所示,a、b、c为三个物块,M、N为两个轻弹簧,N弹簧下端固定在水平地面上,上端与c相连接,N弹簧的上端与b相连接,下端与c相连接,R为跨过定滑轮的轻绳,系统静止,则下列说法中正确的有( )
如图所示,a、b、c为三个物块,M、N为两个轻弹簧,N弹簧下端固定在水平地面上,上端与c相连接,N弹簧的上端与b相连接,下端与c相连接,R为跨过定滑轮的轻绳,系统静止,则下列说法中正确的有( )| A. | 若M被拉伸,则N一定被拉伸 | B. | 若M被压缩,则N一定被压缩 | ||
| C. | 若N被拉伸,则M一定被拉伸 | D. | 若N被压缩,则M一定被压缩 |
11.设回旋加速器中的匀强的磁感应强度为B,粒子的质量为m,所带电荷量为q,刚进入磁场的速度为v0,回旋加速器的最大半径为R,那么两极间所加的交变电压的周期T和该粒子的最大速度v分别为( )
| A. | T=$\frac{2πm}{qB}$,v不超过$\frac{qBR}{m}$ | B. | T=$\frac{πm}{qB}$,v不超过$\frac{qBR}{m}$ | ||
| C. | T=$\frac{2πm}{qB}$,v不超过$\frac{qBR}{2m}$ | D. | T=$\frac{πm}{qB}$,v不超过$\frac{qBR}{2m}$ |
 如图所示,斜面始终静止在地面上,物体A质量为2kg,为使A在斜面上静止,已知物体与斜面间动摩擦因数为0.4,最大静摩擦力等于滑动摩擦力,g=10m/s2.
如图所示,斜面始终静止在地面上,物体A质量为2kg,为使A在斜面上静止,已知物体与斜面间动摩擦因数为0.4,最大静摩擦力等于滑动摩擦力,g=10m/s2.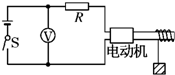 利用电动机通过如图所示的电路提升重物,已知电源电动势E=6V,电源内阻r=1Ω,电阻R=3Ω,重物质量m=0.10kg,当将重物固定时,电压表的示数为5V,当重物不固定,且电动机最后以稳定的速度匀速提升重物时,电压表的示数为5.6V,求:
利用电动机通过如图所示的电路提升重物,已知电源电动势E=6V,电源内阻r=1Ω,电阻R=3Ω,重物质量m=0.10kg,当将重物固定时,电压表的示数为5V,当重物不固定,且电动机最后以稳定的速度匀速提升重物时,电压表的示数为5.6V,求: