题目内容
【题目】（18分）如图所示，水平轨道AB长L=9 m，光滑倾斜轨道BC足够长。开始时质量为
的滑块Q静止在AB中点M处；在A点，质量为
的滑块P以速度
向右运动；P、Q只会发生弹性碰撞，滑块经过B点时，动能损失不计。已知重力加速度g=10 m/s2，P、Q与水平轨道间的动摩擦因数μ=0.1。求：
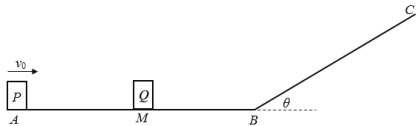
（1）P向右运动的最大位移大小；
（2）Q在倾斜轨道上能滑到的最大高度；
（3）P、Q都停下后两滑块间的距离。
【答案】（1）6.5 m （2）1.35 m （3）5 m
【解析】（1）设P、Q碰撞前瞬间，P的速度为v1，由动能定理有
，解得
（2分）
P、Q发生弹性碰撞，由动量守恒定律有
（2分）
由机械能守恒定律有
（2分）
解得
，
（1分）
P继续向右运动的距离
（1分）
P向右运动的最大位移
（1分）
（2）由动能定理有
（1分）
解得Q在倾斜轨道上能滑到的最大高度h=1.35 m（1分）
（3）假设Q从斜面上滑下来后，会与滑块P发生第二次弹性碰撞。由运动学知识可知Q与P碰前，P已经停下来了。由动能定理有
（1分）
解得P、Q碰前瞬间，Q的速度
（1分）
P、Q间一定发生弹性碰撞，由动量守恒定律有
由机械能守恒定律有
解得
，
，负号表示方向向右（2分）
碰后滑块P向左滑动的位移
（1分）
碰后滑块Q向右滑动的位移
，所以滑块Q在第二次碰撞后会冲上斜面后返回
，不会发生第三次碰撞（1分）
所以P、Q都停下后两滑块相距
（1分）
练习册系列答案
名校课堂系列答案
相关题目
