题目内容
 如图所示的坐标平面内,在y轴的左侧存在垂直纸面向外、磁感应强度大小B1=0.20T的匀强磁场,在y轴的右侧存在垂直纸面向里、宽度d=0.125m的匀强磁场B2.某时刻一质量m=2.0×10-8kg、电量q=+4.0×10-4C的带电微粒(重力可忽略不计),从x轴上坐标为(-0.25m,0)的P点以速度v=2.0×103 m/s沿y轴正方向运动.试求:
如图所示的坐标平面内,在y轴的左侧存在垂直纸面向外、磁感应强度大小B1=0.20T的匀强磁场,在y轴的右侧存在垂直纸面向里、宽度d=0.125m的匀强磁场B2.某时刻一质量m=2.0×10-8kg、电量q=+4.0×10-4C的带电微粒(重力可忽略不计),从x轴上坐标为(-0.25m,0)的P点以速度v=2.0×103 m/s沿y轴正方向运动.试求:(1)微粒在y轴的左侧磁场中运动的轨道半径;
(2)微粒第一次经过y轴时速度方向与y轴正方向的夹角;
(3)要使微粒不能从右侧磁场边界飞出,B2应满足的条件.
分析:(1)由图可知微粒的转动半径,则由牛顿第二定律可求得半径;
(2)根据题意作出粒子的运动轨迹,则由几何关系可得出微粒第一次经过y轴时速度方向与y轴正方向的夹角;
(3)要使粒子不飞出磁场,则如图可知粒子运动的临界值为与边界相切,则由几何关系可得出磁感应强度的范围.
(2)根据题意作出粒子的运动轨迹,则由几何关系可得出微粒第一次经过y轴时速度方向与y轴正方向的夹角;
(3)要使粒子不飞出磁场,则如图可知粒子运动的临界值为与边界相切,则由几何关系可得出磁感应强度的范围.
解答: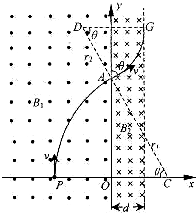 解:(1)设微粒在y轴左侧做匀速圆周运动的半径为r1,转过的圆心角为θ
解:(1)设微粒在y轴左侧做匀速圆周运动的半径为r1,转过的圆心角为θ
由牛顿第二定律可知 qvB1=m
代入数据得 r1=0.5m
(2)粒子在磁场中运动的轨迹如图; 由几何关系得
cosθ=
=
则θ=60°
(3)设粒子恰好不飞出右侧磁场时,磁感应强度为B0,运动半径为r2,其运动轨迹如图 有几何关系得 r2cosθ=r2-dr2=0.25m
由qvB0=m
得 B0=0.4T
所以磁场满足B0≥0.4T
答:(1)轨道半径发为0.5m; (2)角度为60°; (3)磁感应强度应大于等于0.4T.
 解:(1)设微粒在y轴左侧做匀速圆周运动的半径为r1,转过的圆心角为θ
解:(1)设微粒在y轴左侧做匀速圆周运动的半径为r1,转过的圆心角为θ由牛顿第二定律可知 qvB1=m
| v2 |
| r1 |
代入数据得 r1=0.5m
(2)粒子在磁场中运动的轨迹如图; 由几何关系得
cosθ=
| r1-0.25 |
| r1 |
| 1 |
| 2 |
则θ=60°
(3)设粒子恰好不飞出右侧磁场时,磁感应强度为B0,运动半径为r2,其运动轨迹如图 有几何关系得 r2cosθ=r2-dr2=0.25m
由qvB0=m
| v2 |
| r2 |
所以磁场满足B0≥0.4T
答:(1)轨道半径发为0.5m; (2)角度为60°; (3)磁感应强度应大于等于0.4T.
点评:带电粒子在磁场中的运动题目,在应用一些特殊规律解题时,一定要明确规律适用的条件,准确地画出轨迹是关键.

练习册系列答案
相关题目


