题目内容
如图所示的坐标平面内,y轴左侧存在方向垂直纸面向外、磁感应强度大小B1=0.20 T的匀强磁场,在y轴的右侧存在方向垂直纸面向里,宽度d=12.5 cm的匀强磁场B2,某时刻一质量m=2.0×10-8 kg、电荷量q=+4.0×10-4 C的带电微粒(重力可忽略不计),从x轴上坐标为(-0.25 m,0)的P点以速度v0=2.0×103 m/s沿y轴正方向运动.试求:

(1)微粒在y轴左侧磁场中运动的轨道半径;
(2)微粒第一次经过y轴时,速度方向与y轴正方向的夹角;
(3)要使微粒不能从右侧磁场边界飞出,B2应满足的条件.
【答案】
(1)0.5 m (2)60° (3)B2≥0.4 T
【解析】(1)设微粒在y轴左侧匀强磁场中做匀速圆周运动的半径为r1,转过的圆心角为θ,则qv0B1=m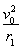
解得r1=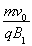 =0.5 m
=0.5 m
(2)粒子在磁场中运动轨迹如图所示,由几何关系得:
cos θ=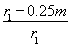 =
=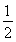 ,则θ=60°.
,则θ=60°.
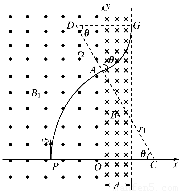
(3)设粒子恰好不飞出右侧磁场时运动半径为r2,其运动轨迹如图所示,由几何关系得
r2cos θ=r2-d
解得r2=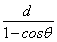 =0.25 m
=0.25 m
由洛伦兹力充当向心力,且粒子运动半径不大于r2,
得:qv0B2≥m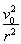
解得:B2≥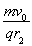 =0.4 T
=0.4 T
即磁感应强度B2应满足:B2≥0.4 T.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示的坐标平面内,在y轴的左侧存在垂直纸面向外、磁感应强度大小B1=0.20T的匀强磁场,在y轴的右侧存在垂直纸面向里、宽度d=0.125m的匀强磁场B2.某时刻一质量m=2.0×10-8kg、电量q=+4.0×10-4C的带电微粒(重力可忽略不计),从x轴上坐标为(-0.25m,0)的P点以速度v=2.0×103 m/s沿y轴正方向运动.试求:
如图所示的坐标平面内,在y轴的左侧存在垂直纸面向外、磁感应强度大小B1=0.20T的匀强磁场,在y轴的右侧存在垂直纸面向里、宽度d=0.125m的匀强磁场B2.某时刻一质量m=2.0×10-8kg、电量q=+4.0×10-4C的带电微粒(重力可忽略不计),从x轴上坐标为(-0.25m,0)的P点以速度v=2.0×103 m/s沿y轴正方向运动.试求:
