题目内容
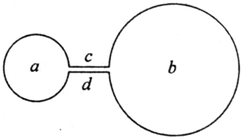如图所示，a、b是两个用同样金属导线制成的圆环，它们的半径比ra：rb=1：2，连接两环的直导线c、d的电阻忽略不计．现有磁感应强度变化率恒定的变化磁场，第一次将a环放入变化的磁场中，测得c、d两导线间的电压为U1．第二次将b环放入变化的磁场中，测得c、d两导线间的电压为U2．两次圆环所在平面均与磁感线垂直，则（ ）分析：a环与b环的半径之比为1：2，故周长之比为1：2，根据电阻定律R=ρ
，电阻之比为1：2；根据法拉第电磁感应定律公式E=n
得到两次电动势的大小关系，然后结合闭合电路欧姆定律分析即可．
| L |
| S |
| △? |
| △t |
解答：解：a环与b环的半径之比为1：2，故周长之比为1：2，根据电阻定律R=ρ
，电阻之比为1：2；
c、d两点间电势差大小为路端电压，为：U=
E；
磁感应强度变化率恒定的变化磁场，故根据法拉第电磁感应定律公式E=n
=
?S，得到两次电动势的大小之比为1：4；
故两次的路段电压之比为U1：U2=RA：RB=1：2，故A正确，BCD错误；
故选A．
| L |
| S |
c、d两点间电势差大小为路端电压，为：U=
| R |
| R+r |
磁感应强度变化率恒定的变化磁场，故根据法拉第电磁感应定律公式E=n
| △? |
| △t |
| △B |
| △t |
故两次的路段电压之比为U1：U2=RA：RB=1：2，故A正确，BCD错误；
故选A．
点评：本题关键是理清电路结构，然后根据闭合电路欧姆定律、电阻定律和法拉第电磁感应定律列式分析，同时理解路端电压的含义．
练习册系列答案
相关题目
如图所示，a、b是两个带有同种电荷的小球，现用两根绝缘细线将它们悬挂于真空中同一点．已知两球静止时，它们离水平地面的高度相等，线与竖直方向的夹角分别为α、β，且α＜β．现有以下判断，其中正确的是（ ）
如图所示，A、B是两块相同的均匀长方形砖块，质量为M，长度L，叠放在一起，且A相对于B的右端伸出
（2011?锦州模拟）如图所示，A、B是两个位于固定斜面上的正方体物块，它们的质量相等，F是沿水平方向作用于A上的外力，已知A与B的接触面，A、B与斜面的接触面均光滑，下列说法正确的是（ ）
如图所示，A，B是两个完全相同的灯泡，L是自感系数较大的线圈，其直流电阻忽略不计．当电键K闭合时，下列说法正确的是（ ）
电风扇的扇叶的重心如果不在转轴上，转动时会使风扇抖动，并加速转轴磨损．调整时，可在扇叶的一区域通过固定小金属块的办法改变其重心位置．如图所示，A、B是两调整重心的金属块（可视为质点），其质量相等，它们到转轴O的距离rA＜rB．扇叶转动后，它们的（ ）| A、向心力FA＜FB | B、线速度大小相等 | C、向心加速度相等 | D、角速度大小相等 |