题目内容
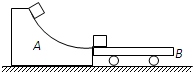 如图所示,A为一具有光滑曲面的固定轨道,轨道底端是水平的,质量M=30kg的小车B静止于轨道右侧,其板面与轨道底端靠近且在同一水平面上,一个质量m=20kg的物体C以3.0m/s的初速度从轨道顶滑下,冲上小车B后经一段时间与小车相对静止并继续一起运动.若轨道顶端与底端水平面的高度差h为0.80m,物体与小车板面间的动摩擦因数μ为0.40,小车与水平面间的摩擦忽略不计,(取g=10m/s2),求:
如图所示,A为一具有光滑曲面的固定轨道,轨道底端是水平的,质量M=30kg的小车B静止于轨道右侧,其板面与轨道底端靠近且在同一水平面上,一个质量m=20kg的物体C以3.0m/s的初速度从轨道顶滑下,冲上小车B后经一段时间与小车相对静止并继续一起运动.若轨道顶端与底端水平面的高度差h为0.80m,物体与小车板面间的动摩擦因数μ为0.40,小车与水平面间的摩擦忽略不计,(取g=10m/s2),求:(1)物体与小车保持相对静止时的速度;
(2)物体冲上小车后相对于小车板面滑动的距离.
分析:(1)物体C下滑过程机械能守恒列出等式,根据物体相对于小车板面滑动过程动量守恒求解
(2)物体相对于小车板面滑动,由能量守恒求解.
(2)物体相对于小车板面滑动,由能量守恒求解.
解答:解:(1)下滑过程机械能守恒:
mgh+
m
=0+
m
①
物体相对于小车板面滑动过程动量守恒
mv2=(m+M)v ②
所以 v=2.0m/s ③
(2)设物体相对于小车板面滑动的距离为L
由能量守恒有,摩擦生热:
Q=μmgL=
m
-
(m+M)v2 ⑤
代入数据解得:L=1.875m
答:(1)物体与小车保持相对静止时的速度是2.0m/s;
(2)物体冲上小车后相对于小车板面滑动的距离是1.875m.
mgh+
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
物体相对于小车板面滑动过程动量守恒
mv2=(m+M)v ②
所以 v=2.0m/s ③
(2)设物体相对于小车板面滑动的距离为L
由能量守恒有,摩擦生热:
Q=μmgL=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
代入数据解得:L=1.875m
答:(1)物体与小车保持相对静止时的速度是2.0m/s;
(2)物体冲上小车后相对于小车板面滑动的距离是1.875m.
点评:该题是一道综合题,综合运用了机械能守恒定律、动量守恒定律以及功能关系,解决本题的关键熟练这些定理、定律的运用.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 如图所示,A为一具有光滑曲面的固定轨道,轨道底端是水平的,质量M=40 kg的小车B静止于轨道右侧,其板面与轨道底端靠近且在同一水平面上,一个质量m=20 kg的物体C以v1=2m/s的初速度从轨道顶滑下,冲上小车B后经一段时与小车相对静止并继续一起运动.若轨道顶端与底端水平面的高度差为h=0.8 m,物体与小车板面间的动摩擦因数为μ=0.40,小车与水平面间的摩擦忽略不计,(取重力加速度g=10 m/s2)求:
如图所示,A为一具有光滑曲面的固定轨道,轨道底端是水平的,质量M=40 kg的小车B静止于轨道右侧,其板面与轨道底端靠近且在同一水平面上,一个质量m=20 kg的物体C以v1=2m/s的初速度从轨道顶滑下,冲上小车B后经一段时与小车相对静止并继续一起运动.若轨道顶端与底端水平面的高度差为h=0.8 m,物体与小车板面间的动摩擦因数为μ=0.40,小车与水平面间的摩擦忽略不计,(取重力加速度g=10 m/s2)求: