题目内容
 如图所示,A为一具有光滑曲面的固定轨道,轨道底端是水平的,质量M=40 kg的小车B静止于轨道右侧,其板面与轨道底端靠近且在同一水平面上,一个质量m=20 kg的物体C以v1=2m/s的初速度从轨道顶滑下,冲上小车B后经一段时与小车相对静止并继续一起运动.若轨道顶端与底端水平面的高度差为h=0.8 m,物体与小车板面间的动摩擦因数为μ=0.40,小车与水平面间的摩擦忽略不计,(取重力加速度g=10 m/s2)求:
如图所示,A为一具有光滑曲面的固定轨道,轨道底端是水平的,质量M=40 kg的小车B静止于轨道右侧,其板面与轨道底端靠近且在同一水平面上,一个质量m=20 kg的物体C以v1=2m/s的初速度从轨道顶滑下,冲上小车B后经一段时与小车相对静止并继续一起运动.若轨道顶端与底端水平面的高度差为h=0.8 m,物体与小车板面间的动摩擦因数为μ=0.40,小车与水平面间的摩擦忽略不计,(取重力加速度g=10 m/s2)求:(1)物体与小车保持相对静止时的速度V;
(2)从物体冲上小车到与小车相对静止所用的时间t;
(3)物体冲上小车后相对于小车板面滑动的距离l.
分析:(1)物块从光滑曲面顶端滑下时,只有重力做功,机械能守恒.根据机械能守恒,得出物块滑到底端时的速度.物块滑上小车的过程中系统所受的外力之和为0,根据动量守恒,得出物块与小车相对静止时的速度V.
(2)物块滑上小车,与小车发生相对滑动的过程中,M所受的合力为m对它的摩擦力,根据动量定理μmgt=MV,求出物体冲上小车到与小车相对静止所用的时间.
(3)在物块滑上小车的过程中,对系统研究,运用功能关系,产生的内能等于系统动能的损失,即μmgl=
m
-
(m+M)V2求出物体冲上小车后相对于小车板面滑动的距离l.
(2)物块滑上小车,与小车发生相对滑动的过程中,M所受的合力为m对它的摩擦力,根据动量定理μmgt=MV,求出物体冲上小车到与小车相对静止所用的时间.
(3)在物块滑上小车的过程中,对系统研究,运用功能关系,产生的内能等于系统动能的损失,即μmgl=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
解答:解:(1)下滑过程机械能守恒,设滑到底端的速度为v2
∵mgh+
m
=0+
m
∴v2=
=2
m/s
根据mv2=(m+M)V
∴V=
=
m/s=
m/s
故物体与小车保持相对静止时的速度V为
m/s.
(2)由动量定理有μmgt=MV
则t=
=
s
故物体冲上小车到与小车相对静止所用的时间t为
s.
(3)由功能关系有μmgl=
m
-
(m+M)
l=
=
m
故物体冲上小车后相对于小车板面滑动的距离l为
m.
∵mgh+
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
∴v2=
|
| 5 |
根据mv2=(m+M)V
∴V=
| mv2 |
| m+M |
20×2
| ||
| 20+40 |
| 2 |
| 3 |
| 5 |
故物体与小车保持相对静止时的速度V为
2
| ||
| 3 |
(2)由动量定理有μmgt=MV
则t=
| MV |
| μmg |
| ||
| 3 |
故物体冲上小车到与小车相对静止所用的时间t为
| ||
| 3 |
(3)由功能关系有μmgl=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| V | 2 ; |
l=
m
| ||
| 2μmg |
| 5 |
| 3 |
故物体冲上小车后相对于小车板面滑动的距离l为
| 5 |
| 3 |
点评:该题是一道综合题,综合运用了机械能守恒定律、动量守恒定律、动量定理以及功能关系,解决本题的关键熟练这些定理、定律的运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
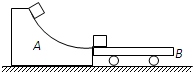 如图所示,A为一具有光滑曲面的固定轨道,轨道底端是水平的,质量M=30kg的小车B静止于轨道右侧,其板面与轨道底端靠近且在同一水平面上,一个质量m=20kg的物体C以3.0m/s的初速度从轨道顶滑下,冲上小车B后经一段时间与小车相对静止并继续一起运动.若轨道顶端与底端水平面的高度差h为0.80m,物体与小车板面间的动摩擦因数μ为0.40,小车与水平面间的摩擦忽略不计,(取g=10m/s2),求:
如图所示,A为一具有光滑曲面的固定轨道,轨道底端是水平的,质量M=30kg的小车B静止于轨道右侧,其板面与轨道底端靠近且在同一水平面上,一个质量m=20kg的物体C以3.0m/s的初速度从轨道顶滑下,冲上小车B后经一段时间与小车相对静止并继续一起运动.若轨道顶端与底端水平面的高度差h为0.80m,物体与小车板面间的动摩擦因数μ为0.40,小车与水平面间的摩擦忽略不计,(取g=10m/s2),求: