题目内容
17.质量为m的球A以速度v0与原来静止的质量为3m的B球做对心碰撞,设碰后的速度分别为vA和vB,则下列各组数据中可能的是( )| A. | vA=$\frac{{v}_{0}}{4}$、vB=$\frac{{v}_{0}}{4}$ | B. | vA=v0、vB=$\frac{2{v}_{0}}{3}$ | ||
| C. | vA=$\frac{{v}_{0}}{2}$、vB=$\frac{2{v}_{0}}{3}$ | D. | vA=$\frac{{v}_{0}}{2}$、vB=$\frac{{v}_{0}}{6}$ |
分析 两球碰撞过程系统动量守恒,应用动量守恒定律求出碰撞后两球的速度,然后分析答题.
解答 解:A、两球组成的系统动量守恒,以A的初速度方向为正方向,如果碰撞是完全非弹性碰撞,由动量守恒定律得:mv0=(m+3m)v,解得:vA=vB=v=$\frac{{v}_{0}}{4}$,故A正确;
B、如果碰撞为完全弹性碰撞,以A的初速度方向为正方向,由动量守恒定律得:mv0=mvA+3mvB,由机械能守恒定律得:$\frac{1}{2}$mv02=$\frac{1}{2}$mvA2+$\frac{1}{2}$•3mvB2,vA=-$\frac{1}{2}$v0,vB=$\frac{1}{2}$v0,则:-$\frac{1}{2}$v0≤vA≤$\frac{1}{4}$v0,$\frac{1}{4}$v0≤vB≤$\frac{1}{2}$v0,BC错误,D正确;
故选:AD.
点评 本题考查了求碰撞后球的速度,分析清楚球的运动过程,应用动量守恒定律可以解题,解题时注意正方向的选择.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
7.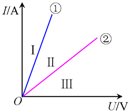 如图所示是两个不同电阻的I-U图象,则图象①②表示的电阻及两电阻串联或并联后的I-U图象所在区域分别是( )
如图所示是两个不同电阻的I-U图象,则图象①②表示的电阻及两电阻串联或并联后的I-U图象所在区域分别是( )
 如图所示是两个不同电阻的I-U图象,则图象①②表示的电阻及两电阻串联或并联后的I-U图象所在区域分别是( )
如图所示是两个不同电阻的I-U图象,则图象①②表示的电阻及两电阻串联或并联后的I-U图象所在区域分别是( )| A. | ①表示大电阻值的图象,并联后在区域III | |
| B. | ①表示小电阻值的图象,并联后在区域Ⅱ | |
| C. | ②表示大电阻值的图象,并联后在区域Ⅱ | |
| D. | ②表示大电阻值的图象,串联后在区域III |
8.关于弹力,下列说法正确的是( )
| A. | 弹力可以产生在两个不接触的物体之间 | |
| B. | 两个接触的物体之间一定有弹力 | |
| C. | 有弹力一定有摩擦力 | |
| D. | 有摩擦力一定有弹力 |
5.下列物品中必须用到磁性材料的是( )
| A. | 录象带 | B. | 计算机上的磁盘 | ||
| C. | 银行的信用卡 | D. | 喝水用的搪瓷杯子 |
12.一质量为2kg的滑块,以4m/s的速度在光滑水平面上向左滑行,从某一时刻起,在滑块上作用一向右的水平力,经过一段时间,滑块的速度方向变为向右,大小为4m/s,在这段时间里水平力的冲量大小为( )
| A. | 0 | B. | 8N•s | C. | 16N•s | D. | 32N•s |
2.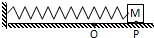 如图所示,轻弹簧的左端固定在墙上,右端固定在放于粗糙水平面的物块M上,当物块处在O处时弹簧处于自然状态,现将物块拉至P点后释放,则物块从P点返回O处的过程中( )
如图所示,轻弹簧的左端固定在墙上,右端固定在放于粗糙水平面的物块M上,当物块处在O处时弹簧处于自然状态,现将物块拉至P点后释放,则物块从P点返回O处的过程中( )
 如图所示,轻弹簧的左端固定在墙上,右端固定在放于粗糙水平面的物块M上,当物块处在O处时弹簧处于自然状态,现将物块拉至P点后释放,则物块从P点返回O处的过程中( )
如图所示,轻弹簧的左端固定在墙上,右端固定在放于粗糙水平面的物块M上,当物块处在O处时弹簧处于自然状态,现将物块拉至P点后释放,则物块从P点返回O处的过程中( )| A. | 物块的速度不断增大,而加速度不断减小 | |
| B. | 物块的速度先增后减,而加速度先减后增 | |
| C. | 物块的速度不断减小,而加速度不断增大 | |
| D. | 物块的速度先增后减,而加速度不断减小 |
6.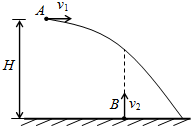 如图所示,甲从高H处以初速度v1水平抛出小球A,乙同时从地面以初速度v2竖直上抛小球B,在B尚未到达最高点之前,两球在空中相遇,则( )
如图所示,甲从高H处以初速度v1水平抛出小球A,乙同时从地面以初速度v2竖直上抛小球B,在B尚未到达最高点之前,两球在空中相遇,则( )
 如图所示,甲从高H处以初速度v1水平抛出小球A,乙同时从地面以初速度v2竖直上抛小球B,在B尚未到达最高点之前,两球在空中相遇,则( )
如图所示,甲从高H处以初速度v1水平抛出小球A,乙同时从地面以初速度v2竖直上抛小球B,在B尚未到达最高点之前,两球在空中相遇,则( )| A. | 从抛出到两球相遇所用时间为t=$\frac{H}{v_1}$ | |
| B. | 抛出前两球的水平距离s=$\frac{{H{v_1}}}{v_2}$ | |
| C. | 相遇时A球速率vA=$\frac{gH}{v_2}$ | |
| D. | 若v2=$\sqrt{gH}$,则两球相遇在$\frac{H}{2}$处 |
7.关于自由落体运动,下列说法中正确的是( )
| A. | 在空气中,不考虑空气阻力的运动是自由落体运动 | |
| B. | 物体做自由落体运动时不受任何外力作用 | |
| C. | 质量大的物体受到的重力大,落到地面时的速度也大 | |
| D. | 自由落体运动是初速度为零的匀加速运动 |
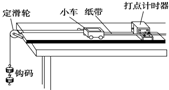 某同学把附有滑轮的长木板放在实验桌上,将细绳一端拴在小车上,另一端绕过定滑轮,挂上适当的钩码,使小车在钩码的牵引下运动,以此定量探究绳拉力做功与小车速度变化的关系,此外还准备了打点计时器及配套的电源、导线、复写纸、纸带、小木块等.组装的实验装置如图所示.
某同学把附有滑轮的长木板放在实验桌上,将细绳一端拴在小车上,另一端绕过定滑轮,挂上适当的钩码,使小车在钩码的牵引下运动,以此定量探究绳拉力做功与小车速度变化的关系,此外还准备了打点计时器及配套的电源、导线、复写纸、纸带、小木块等.组装的实验装置如图所示.