题目内容
如图甲所示,B为电源,电动势E=75V,内阻不计.R1为固定电阻,R2为光敏电阻.C为平行板电容器,虚线OO′到两极板距离相等,极板长l=6.0×10-2m,两极板的间距d=1.0×10-2m.P为一圆盘,由形状相同、透光率不同的两个半圆形透光片a和b构成,它绕AA′轴按图中箭头方向匀速转动.当细光束通过不同的透光片照射光敏电阻R2时,R2的阻值不同.有一细电子束沿OO′以速度v0=2.0×107m/s连续不断地射入平行板电容器C,电子发生偏转.平行板电容器右端有一接收屏S,电子打到屏上的位置与OO′的距离记为y.当光束刚开始通过透光片a照射R2时取t=0,随着圆盘转动,y随时间t变化的关系如图乙所示.忽略细光束的宽度,忽略电容器的充、放电时间以及电子所受的重力.假设照在R2上的光强发生改变时R2阻值立即有相应的改变.

(1)求圆盘P匀速转动的角速度ω;
(2)已知电子的电荷量e=1.6×10-19C,电子的质量m=9×10-31kg.当细光束通过透光片a照射光敏电阻R2时,R2的阻值为1000Ω,当细光束通过透光片b照射光敏电阻R2时,R2的阻值小于1000Ω.
Ⅰ.定值电阻R1的阻值;
Ⅱ.光束通过透光片b照射R2时,R2的阻值应满足什么条件?

(1)求圆盘P匀速转动的角速度ω;
(2)已知电子的电荷量e=1.6×10-19C,电子的质量m=9×10-31kg.当细光束通过透光片a照射光敏电阻R2时,R2的阻值为1000Ω,当细光束通过透光片b照射光敏电阻R2时,R2的阻值小于1000Ω.
Ⅰ.定值电阻R1的阻值;
Ⅱ.光束通过透光片b照射R2时,R2的阻值应满足什么条件?
分析:1、根据乙图可知周期T,再根据角速度与周期的关系ω=
,代入竖直可知圆盘P匀速转动的角速度.
2、电子在电场中做类平抛运动,运用牛顿第二定律、运动学公式,结合分解的方法可以得到电子偏转距离的表达式,进一步计算出电容器两极板之间的电压.因为直接电流不能通过电容器,故电容器两端的电压与R1两端的电压相等,由R1和R2串联,可以根据闭合电路欧姆定律求得R1的阻值.
3、电子刚好射不出电容器时,此时R2的阻值为最大,设为根据上述思路计算出最大值R0即可.
| 2π |
| T |
2、电子在电场中做类平抛运动,运用牛顿第二定律、运动学公式,结合分解的方法可以得到电子偏转距离的表达式,进一步计算出电容器两极板之间的电压.因为直接电流不能通过电容器,故电容器两端的电压与R1两端的电压相等,由R1和R2串联,可以根据闭合电路欧姆定律求得R1的阻值.
3、电子刚好射不出电容器时,此时R2的阻值为最大,设为根据上述思路计算出最大值R0即可.
解答:解:(1)由题意可知,圆盘转动的周期T=4s,则其角速度ω=
=
rad/s
(2)Ⅰ.电容器的电压U1=
E----①
设电子在电容器中运动的时间为t,则在沿极板方向有l=v0t--②
在垂直于极板方向y=
?
?t2--③
联立①②③,代入y=2×10-3m及其他数据可得R1=500Ω
Ⅱ.设R2的阻值为R0时,电子刚好射不出电容器,此时y0=
=5.0×10-3m,电容器两极板间的电压为U0.
同上有:U0=
E----④
水平方向匀速运动l=v0t----⑤
竖直方向匀加速运动y0=
?
?t2----⑥
联立④⑤⑥,代入数据可得R0=100Ω
所以R2的阻值应满足的条件是R2≤100Ω
答:(1)圆盘P匀速转动的角速度ω为
rad/s;
(2)Ⅰ.定值电阻R1的阻值为5000Ω;Ⅱ.光束通过透光片b照射R2时,R2的阻值应R2≤100Ω.
| 2π |
| T |
| π |
| 2 |
(2)Ⅰ.电容器的电压U1=
| R1 |
| R1+R2 |
设电子在电容器中运动的时间为t,则在沿极板方向有l=v0t--②
在垂直于极板方向y=
| 1 |
| 2 |
| eU |
| md |
联立①②③,代入y=2×10-3m及其他数据可得R1=500Ω
Ⅱ.设R2的阻值为R0时,电子刚好射不出电容器,此时y0=
| d |
| 2 |
同上有:U0=
| R1 |
| R1+R0 |
水平方向匀速运动l=v0t----⑤
竖直方向匀加速运动y0=
| 1 |
| 2 |
| eU0 |
| md |
联立④⑤⑥,代入数据可得R0=100Ω
所以R2的阻值应满足的条件是R2≤100Ω
答:(1)圆盘P匀速转动的角速度ω为
| π |
| 2 |
(2)Ⅰ.定值电阻R1的阻值为5000Ω;Ⅱ.光束通过透光片b照射R2时,R2的阻值应R2≤100Ω.
点评:本题着重考查带电粒子在电场中的偏转问题,弄清什么力使粒子产生加速度,在求整个偏转的过程中,要注意情况讨论粒子的运动形式,根据需要分步讨论计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
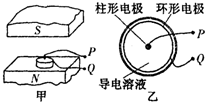 如图甲所示,上端为S极、下端为N极,把一个圆形玻璃皿放入磁场中,玻璃皿的中心放一个圆柱形电极P,沿边缘内壁放一个圆环形电极Q,然后在玻璃中放入含正、负离子的导电溶液.图2是俯视图,若将电极与电源相连,则溶液中离子的运动情况是( )
如图甲所示,上端为S极、下端为N极,把一个圆形玻璃皿放入磁场中,玻璃皿的中心放一个圆柱形电极P,沿边缘内壁放一个圆环形电极Q,然后在玻璃中放入含正、负离子的导电溶液.图2是俯视图,若将电极与电源相连,则溶液中离子的运动情况是( )



