题目内容
2. 如图,两个侧壁绝热、顶部和底部都导热的相同汽缸直立放置,汽缸底部和顶部均有细管连通,顶部的细管带有阀门K.两汽缸的容积均为V0,汽缸中各有一个绝热活塞(质量不同,厚度可忽略).开始时K关闭,两活塞下方和右活塞上方充有气体(可视为理想气体),压强分别为p0和$\frac{{ρ}_{0}}{3}$;左活塞在汽缸正中间,其上方为真空; 右活塞上方气体体积为$\frac{{v}_{0}}{4}$.现使汽缸底与一恒温热源接触,平衡后左活塞升至汽缸顶部,且与顶部刚好没有接触;然后打开K,经过一段时间,重新达到平衡.已知外界温度为T0,不计活塞与汽缸壁间的摩擦.求:
如图,两个侧壁绝热、顶部和底部都导热的相同汽缸直立放置,汽缸底部和顶部均有细管连通,顶部的细管带有阀门K.两汽缸的容积均为V0,汽缸中各有一个绝热活塞(质量不同,厚度可忽略).开始时K关闭,两活塞下方和右活塞上方充有气体(可视为理想气体),压强分别为p0和$\frac{{ρ}_{0}}{3}$;左活塞在汽缸正中间,其上方为真空; 右活塞上方气体体积为$\frac{{v}_{0}}{4}$.现使汽缸底与一恒温热源接触,平衡后左活塞升至汽缸顶部,且与顶部刚好没有接触;然后打开K,经过一段时间,重新达到平衡.已知外界温度为T0,不计活塞与汽缸壁间的摩擦.求:(1)恒温热源的温度T;
(2)重新达到平衡后左汽缸中活塞上方气体的体积Vx.
分析 (1)两活塞下方封闭的气体等压变化,利用盖吕萨克定律列式求解;
(2)分别以两部分封闭气体,利用玻意耳定律列式求解.
解答 解:(1)与恒温热源接触后,在K未打开时,右活塞不动,两活塞下方的气体经历等压过程,
由盖吕•萨克定律得:$\frac{\frac{5}{4}{V}_{0}}{{T}_{0}}$=$\frac{\frac{7}{4}{V}_{0}}{T}$…①
解得:T=$\frac{7}{5}$T0…②
(2)由初始状态的力学平衡条件可知,左活塞的质量比右活塞的大.
打开K后,左活塞必须升至气缸顶才能满足力学平衡条件.
气缸顶部与外界接触,底部与恒温热源接触,两部分气体各自经历等温过程,
设在活塞上方气体压强为p,由玻意耳定律得:pV0=$\frac{{p}_{0}}{3}$•$\frac{{V}_{x}}{4}$…③
对下方气体由玻意耳定律得:(p+p0)(2V0-Vx)=p0•$\frac{7}{4}$V0…④
联立③④式得:6VX2-V0VX-V02=0,
解得:VX=$\frac{1}{2}$V0,VX=-$\frac{1}{3}$V0不合题意,舍去.
答:(1)恒温热源的温度T为$\frac{7}{5}$T0;
(2)重新达到平衡后左汽缸中活塞上方气体的体积Vx为$\frac{1}{2}$V0.
点评 本题涉及两部分气体状态变化问题,除了隔离研究两部分之外,关键是把握它们之间的联系,比如体积关系、温度关系及压强关系.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
12. 如图所示,某同学通过滑轮组将一重物缓慢吊起的过程中,设该同学对绳的拉力为T,两绳子对滑轮拉力的合力为F,滑轮与绳的重力及摩擦不计,则( )
如图所示,某同学通过滑轮组将一重物缓慢吊起的过程中,设该同学对绳的拉力为T,两绳子对滑轮拉力的合力为F,滑轮与绳的重力及摩擦不计,则( )
 如图所示,某同学通过滑轮组将一重物缓慢吊起的过程中,设该同学对绳的拉力为T,两绳子对滑轮拉力的合力为F,滑轮与绳的重力及摩擦不计,则( )
如图所示,某同学通过滑轮组将一重物缓慢吊起的过程中,设该同学对绳的拉力为T,两绳子对滑轮拉力的合力为F,滑轮与绳的重力及摩擦不计,则( )| A. | T不变 | B. | T越来越小 | C. | F先变大后变小 | D. | F不变 |
11.交变电流是( )
| A. | 矩形线圈绕垂直于磁场方向的轴在匀强磁场中匀速转动时产生的电流 | |
| B. | 按正弦规律变化的电流 | |
| C. | 按余弦规律变化的电流 | |
| D. | 大小、方向随时间做周期性变化的电流 |
13.下列对红外线的作用和来源叙述正确的是( )
| A. | 一切物体都在不停地辐射红外线 | B. | 红外线有很强的荧光效应 | ||
| C. | 红外线最显著的作用是热作用 | D. | 红外线容易穿透云雾烟尘 |
 有一质量为m、电荷量为q的带正电的小球停在绝缘平面上,并处在磁感应强度为B、方向垂直指向纸面内部的匀强磁场中,如图所示,为了使小球飘离平面,匀强磁场在纸面内移动的最小速度应为多少?方向如何?
有一质量为m、电荷量为q的带正电的小球停在绝缘平面上,并处在磁感应强度为B、方向垂直指向纸面内部的匀强磁场中,如图所示,为了使小球飘离平面,匀强磁场在纸面内移动的最小速度应为多少?方向如何? 如图所示,磁铁的磁极吸引着两根细铁丝,两铁丝下端相斥,这是因为铁丝被磁化后,远离磁铁磁极的一端极性相同,由于同名磁极相互排斥而远离.
如图所示,磁铁的磁极吸引着两根细铁丝,两铁丝下端相斥,这是因为铁丝被磁化后,远离磁铁磁极的一端极性相同,由于同名磁极相互排斥而远离.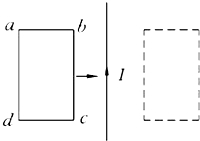 如图所示,线框与通电直导线均位于水平面内,当线框abcd由实线位置在水平面内向右平动,逐渐移动到虚线位置,穿过线框的磁通量如何变化?
如图所示,线框与通电直导线均位于水平面内,当线框abcd由实线位置在水平面内向右平动,逐渐移动到虚线位置,穿过线框的磁通量如何变化?