题目内容
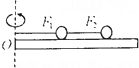
如图所示,厚度不计的薄板A长L=5.0m,质量M=5.0kg,放在水平桌面上,板的右端与桌边相齐.在A上距右端s=3.0m处放一物体B(大小不计),其质量m=2.0kg,已知A、B间的动摩擦因数μ=0.1,A与桌面间和B与桌面间的动摩擦因数μ=0.2,原来系统静止.现在在板的右端施加一大小一定的水平力F=26N,持续作用在A上,将A从B下抽出.(g=10m/s2)求:
(1)A从B下抽出前A、B的加速度各是多少?
(2)B运动多长时间离开A?
(3)物体B最后停在哪里?

(1)A从B下抽出前A、B的加速度各是多少?
(2)B运动多长时间离开A?
(3)物体B最后停在哪里?

(1)对于B,在未离开A时,其运动加速度大小为:aB=
=μ1g=1m/s2
对于A,根据牛顿第二定律得:
F-μ1mg-μ2(m+M)g=MaA
解得:aA=2m/s2
(2)设经过时间t,A离开B,则有:
xA=
aAt2
xB=
aBt2
而xA-xB=L-s
带入数据解得:t=2s
(3)设B从A上掉下时,其速度为v,则
v=aBt=2m/s
xB=
aBt2=
×1×4m=2m
B从A上掉下后,B在桌面的摩擦力作用下做减速运动,其加速度大小为
a2=
=μ1g=2m/s2
运动的位移为:x2=
=
m=1m
所以B运动的总位移为:x=2m+1m=3m
所以物体B最后停在离桌边2m的位置上.
答:(1)A从B下抽出前A的加速度为2m/s2,B的加速度为1m/s2;
(2)B运动2s离开A;
(3)物体B最后停在离桌边2m的位置上.
| μ1mg |
| m |
对于A,根据牛顿第二定律得:
F-μ1mg-μ2(m+M)g=MaA
解得:aA=2m/s2
(2)设经过时间t,A离开B,则有:
xA=
| 1 |
| 2 |
xB=
| 1 |
| 2 |
而xA-xB=L-s
带入数据解得:t=2s
(3)设B从A上掉下时,其速度为v,则
v=aBt=2m/s
xB=
| 1 |
| 2 |
| 1 |
| 2 |
B从A上掉下后,B在桌面的摩擦力作用下做减速运动,其加速度大小为
a2=
| μ2Mg |
| M |
运动的位移为:x2=
| v2 |
| 2a2 |
| 4 |
| 4 |
所以B运动的总位移为:x=2m+1m=3m
所以物体B最后停在离桌边2m的位置上.
答:(1)A从B下抽出前A的加速度为2m/s2,B的加速度为1m/s2;
(2)B运动2s离开A;
(3)物体B最后停在离桌边2m的位置上.

练习册系列答案
相关题目