题目内容
【题目】如图,直角三角形ABC为一棱镜的横截面,∠A=90°,∠B=30°。一束光线平行于底边BC射到AB边上并进入棱镜,然后垂直于AC边射出。
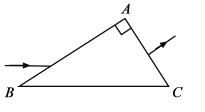
(1)求棱镜的折射率;
(2)保持AB边上的入射点不变,逐渐减小入射角,直到BC边上恰好有光线射出。求此时AB边上入射角的正弦。
【答案】(1)![]() ;(2)sin
;(2)sin![]() =
=![]()
【解析】
(1)光路图及相关量如图所示。光束在AB边上折射,由折射定律得
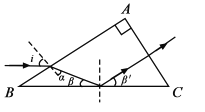
![]() ①
①
式中n是棱镜的折射率。由几何关系可知
α+β=60°②
由几何关系和反射定律得
![]() ③
③
联立①②③式,并代入i=60°得
n=![]() ④
④
(2)设改变后的入射角为![]() ,折射角为
,折射角为![]() ,由折射定律得
,由折射定律得
![]() =n⑤
=n⑤
依题意,光束在BC边上的入射角为全反射的临界角![]() ,且
,且
sin![]() =
=![]() ⑥
⑥
由几何关系得
![]() =α'+30° ⑦
=α'+30° ⑦
由④⑤⑥⑦式得入射角的正弦为
sin![]() =
=![]() ⑧
⑧

练习册系列答案
相关题目