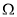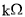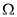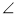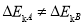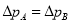题目内容
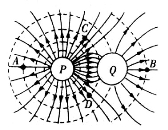
如图所示，小滑块A和B（可视为质点）套在固定的水平光滑杆上。一轻弹簧上端固定在P点，下端与滑块B相连接。现使滑块B静止在P点正下方的O点，O、P间的距离为h。某时刻，滑块A以初速度v0沿杆向右运动，与B碰撞后，粘在一起以O为中心位置做往复运动。光滑杆上的M点与O点间的距离为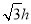
。已知滑块A的质量为2m，滑块B的质量为m，弹簧的原长为
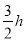，劲度系数
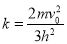。弹簧弹性势能的表达式为
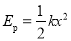（式中k为弹簧的劲度系数，x为弹簧的形变量）。求：
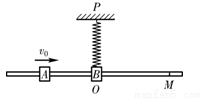
（1）滑块A与滑块B碰后瞬间共同速度v的大小；
（2）当滑块A、B运动到M点时，加速度a的大小；
（3）滑块A、B在往复运动过程中，最大速度vm的大小。
（1）
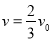（2）
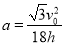（3）
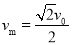
【解析】
试题分析：（1）取A、B滑块为系统，由动量守恒定律有
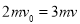
所以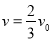 
（4分）
（2）当滑块运动到M点时，弹簧的长度
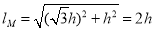
此时弹簧的弹力
根据牛顿第二定律
（6分）
（3）当弹簧处于原长时，滑块的速度最大。取滑块A、B和弹簧为系统，由机械能守恒定律有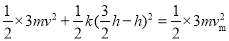 
所以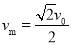 
（8分）
考点：胡克定律 动量守恒定律 功能关系
练习册系列答案
相关题目
