Question

【题目】水平面内有一等边三角形ABC，O点为三角形的几何中心，D点为O点正上方的一点，O点到A、B、C、D四点的距离均为l。现将三个电荷量均为Q的正点电荷分别固定在A、B、C处，已知静电力常量为k。则下列说法正确的是

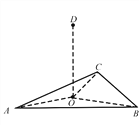
A. O点的电场强度大小

B. D点的电场强度大小

C. O点的电势为零

D. D点的电势比O点的电势低

Answer 1

【答案】D

【解析】A、三个电荷量均为Q的正点电荷在O点产生的电场强度的大小均为，方向互成120°，由点电荷的电场叠加原理和对称性可知O点的电场强度大小为零，故选项A错误；

B、三个电荷量均为Q的正点电荷在D点产生的电场强度的大小均为，方向与OD均成45°，根据对称性可知D点电场强度的方向沿OD方向，根据叠加原理可求出D点的电场强度为，故B错误；

CD、以无穷远处为零电势点，正电荷周围空间电势为正值，可判断O点的电势不为零，又因为沿着电场线方向电势降低，故D点的电势比O点的电势低，故C错误，D正确；

故选D。