题目内容
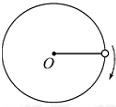一质量为m的小球A用轻绳系于O点，如果给小球一个初速度使其在竖直平面内做圆周运动，某时刻小球A运动的圆轨道的水平直径的右端点时，如图所示位置，其加速度大小为| 17 |
分析：结合小球在水平位置的加速度，通过平行四边形定则求出小球在水平位置的速度，根据机械能守恒定律求出小球在最低点时的速度，根据牛顿第二定律求出绳对小球的拉力大小．
解答：解：设小球在水平直径右端时的速度为V1，由已知条件：a水平=
，而a合=
，得v12=4gr．
设小球在最低点时的速度为v2，
则由机械能守恒得：
mv12+mgr=
mv22，
在最低点：F-mg=
，由以上两式可解得：F=7mg，故B正确．A、C、D错误．
故选B．
| v12 |
| r |
|
设小球在最低点时的速度为v2，
则由机械能守恒得：
| 1 |
| 2 |
| 1 |
| 2 |
在最低点：F-mg=
| mv22 |
| r |
故选B．
点评：本题考查了牛顿第二定律和机械能守恒定律的综合运用，知道小球在水平位置的加速度所受的加速度为合加速度，通过平行四边形定则求出向心加速度．
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
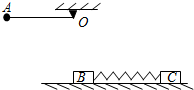如图所示，一质量为m的小球A用长度为l的轻绳系在O处，开始时绳处于水平伸直状态，O处正下方有一质量为
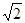g．则它运动到最低点时，绳对球的拉力大小为 ( )
m的物体B，物体B和C用轻质弹簧相连，放置于光滑水平面上，C的质量为
m，现将A由静止释放，A运动到最低点与B发生正碰，碰后AB分开，A运动到最高点时OA连线与竖直方向成600角，重力加速度为g。求：
g，则它运动到最低点时，绳对球的拉力大小为（ ）
）mg
）mg