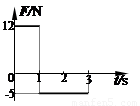题目内容
(18分)如图,粗糙斜面与光滑水平面通过光滑小圆弧平滑连接,斜面倾角θ=37°。A、B是两个质量均为m=l kg的小滑块(可看作质点),B的左端连接一轻质弹簧。若滑块A在斜面上受 到F=4 N,方向垂直斜面向下的恒力作用时,恰能沿斜面匀速下滑。现撤去F,让滑块A从斜面上距斜面底端L=1m处由静止开始下滑。(取g=10 m/s2,sin37°=0.6,cos37°=0.8。)
(1)求滑块A与斜面间的动摩擦因数;
(2)求滑块A到达斜面底端时的速度大小;
(3)滑块A与弹簧接触后粘连在一起,求此后弹簧的最大弹性势能。
(1)0.5(2)2 m/s(3)Ep=1 J
解析:(1)滑块沿斜面匀速下滑时受力如右图所示
根据牛顿第二定律
mgsinθ=μN ((2分)
N=mgcosθ+F(2分)
解得 μ==0.5。(2分)
滑块沿斜面加速下滑时受力如图所示设滑块滑到斜面底端时的速度为v1,根据动能定理
(mgsinθ-μmgcosθ)L= ![]() (3分)
(3分)
代入数据解得 v1=2 m/s。(3分)
(3)以A、B、弹簧为研究对象,设它们共同的速度为v2,根据动量守恒定律
mv1=2mv2(2分)
设弹簧的最大弹性势能为Ep,根据能量守恒 mv12=![]() ×2mv22+Ep(2分)
×2mv22+Ep(2分)
代入数据解得 Ep=1 J。(2分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

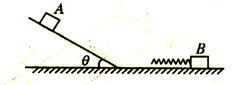

 ”型木块放在光滑水平地面上,木块水平表面AB粗糙,光滑表面BC且与水平面夹角为θ=37°.木块右侧与竖直墙壁之间连接着一个力传感器,当力传感器受压时,其示数为正值;当力传感器被拉时,其示数为负值.一个可视为质点的滑块从C点由静止开始下滑,运动过程中,传感器记录到的力和时间的关系如图(b)所示.已知sin37°=0.6,cos37°=0.8,g取10m/s2.求:
”型木块放在光滑水平地面上,木块水平表面AB粗糙,光滑表面BC且与水平面夹角为θ=37°.木块右侧与竖直墙壁之间连接着一个力传感器,当力传感器受压时,其示数为正值;当力传感器被拉时,其示数为负值.一个可视为质点的滑块从C点由静止开始下滑,运动过程中,传感器记录到的力和时间的关系如图(b)所示.已知sin37°=0.6,cos37°=0.8,g取10m/s2.求: