题目内容
6.2015年6月28日,为执行国际空间站货运补给任务的美国猎鹰9火箭发射升空2分钟后爆炸.假设运载火箭刚开始点火升空时以加速度大小为15m/s2由静止从地面竖直上升,第4s末从运载火箭掉出一小重物,(忽略空气阻力,$\sqrt{15}$=3.87,g=10m/s2)求:(1)小重物最高可上升到距地面多高处?
(2)小重物从运载火箭上掉出之后经多少时间落回地面?
分析 (1)前4s小物体做初速度为零的匀加速直线运动,小重物掉出后以60m/s的初速度做竖直上抛运动,末速度为零时上升到最高,根据匀变速直线运动的规律求解位移,两段位移之和为距地面的高度;
(2)小重物掉出后以60m/s的初速度做竖直上抛运动,分为上升的匀减速直线运动和下降的自由落体运动,分别根据速度时间和位移时间关系求解时间.
解答 解:(1)前4s小物体做初速度为零的匀加速直线运动,加速度a=15m/s2,方向向上.
4s末运载火箭与小物体的速度为:v=at=60m/s
位移为x1=$\frac{1}{2}$at2=120m
小重物掉出后以60m/s的初速度做竖直上抛运动,上升的高度为:
h=$\frac{{v}^{2}}{2g}$=180m
小重物最高可上升到距地面H=x1+h=300m
(2)小重物从运载火箭上脱落后上升所用时间:t1=$\frac{v}{g}$=6s
设从最高点下落到地面的时间为t2,则:H=$\frac{1}{2}g{t}_{2}^{2}$
即300m=$\frac{1}{2}g{t}_{2}^{2}$
t2=$\sqrt{60}$s=2$\sqrt{15}$s=7.74s
则小重物从运载火箭上掉出之后到落回地面需要的时间:t总=t1+t2=13.74s
答:(1)小重物最高可上升到距地面300m高;
(2)小重物从运载火箭上掉出之后经13.74s落回地面.
点评 对于竖直上抛运动,可以分阶段分析物体的运动过程,也可以全过程视为匀变速直线运动,注意规定正方向,做到有条不紊,熟练掌握运动学公式是解决此类问题的基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.两个质量不同的物体从同一高度同时做自由落体运动,下列判断正确的是( )
| A. | 质量大的物体先落地 | B. | 两物体同时落地 | ||
| C. | 两物体落地时的速度相同 | D. | 质量大的物体落地时的速度较大 |
14. 如图所示•两个带正电的粒子P、Q(重力不计)分别以2v、v的速度垂直磁场方向射入扇形匀强磁场区域(边界为$\frac{1}{4}$圆弧,O点为圆心),两粒子速度方向平行,其中速度为2v的粒子P沿半径AO方向射入磁场,速度为v的粒子Q从C点进入磁场,C到AO的距离正好等于磁场边界圆的一半.若两粒子都从D点离开磁场,则( )
如图所示•两个带正电的粒子P、Q(重力不计)分别以2v、v的速度垂直磁场方向射入扇形匀强磁场区域(边界为$\frac{1}{4}$圆弧,O点为圆心),两粒子速度方向平行,其中速度为2v的粒子P沿半径AO方向射入磁场,速度为v的粒子Q从C点进入磁场,C到AO的距离正好等于磁场边界圆的一半.若两粒子都从D点离开磁场,则( )
 如图所示•两个带正电的粒子P、Q(重力不计)分别以2v、v的速度垂直磁场方向射入扇形匀强磁场区域(边界为$\frac{1}{4}$圆弧,O点为圆心),两粒子速度方向平行,其中速度为2v的粒子P沿半径AO方向射入磁场,速度为v的粒子Q从C点进入磁场,C到AO的距离正好等于磁场边界圆的一半.若两粒子都从D点离开磁场,则( )
如图所示•两个带正电的粒子P、Q(重力不计)分别以2v、v的速度垂直磁场方向射入扇形匀强磁场区域(边界为$\frac{1}{4}$圆弧,O点为圆心),两粒子速度方向平行,其中速度为2v的粒子P沿半径AO方向射入磁场,速度为v的粒子Q从C点进入磁场,C到AO的距离正好等于磁场边界圆的一半.若两粒子都从D点离开磁场,则( )| A. | 两粒子运动的轨道半径不相等 | B. | 两粒子在磁场中运动的时间相等 | ||
| C. | P、Q两粒子的比荷之比1:2 | D. | P、Q两粒子的比荷之比2:1 |
1.一物体作直线运动的v-t图线如图所示,则( )


| A. | 前3秒内和前4秒内位移相等 | B. | 前4秒内位移为零 | ||
| C. | 第2秒末物体的加速度改变方向 | D. | 第4秒末物体的速度改变方向 |
11. 倾角为θ=37°的斜面体固定在水平地面上,一个重为100N的光滑球在水平恒力F的作用下,静止在斜面上,若将水平恒力F和斜面体对小球的支持力看成一个力,这个力的大小是( ) (g取10m/s2,sin37°=0.6,cos37°=0.8)
倾角为θ=37°的斜面体固定在水平地面上,一个重为100N的光滑球在水平恒力F的作用下,静止在斜面上,若将水平恒力F和斜面体对小球的支持力看成一个力,这个力的大小是( ) (g取10m/s2,sin37°=0.6,cos37°=0.8)
 倾角为θ=37°的斜面体固定在水平地面上,一个重为100N的光滑球在水平恒力F的作用下,静止在斜面上,若将水平恒力F和斜面体对小球的支持力看成一个力,这个力的大小是( ) (g取10m/s2,sin37°=0.6,cos37°=0.8)
倾角为θ=37°的斜面体固定在水平地面上,一个重为100N的光滑球在水平恒力F的作用下,静止在斜面上,若将水平恒力F和斜面体对小球的支持力看成一个力,这个力的大小是( ) (g取10m/s2,sin37°=0.6,cos37°=0.8)| A. | 60N | B. | 80N | C. | 100N | D. | 120N |
18.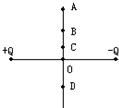 如图所示,在等量异种电荷连线的中垂线上取A、B、C、D四点,B、D两点关于O点对称,则关于各点场强的关系,下列说法中正确的是( )
如图所示,在等量异种电荷连线的中垂线上取A、B、C、D四点,B、D两点关于O点对称,则关于各点场强的关系,下列说法中正确的是( )
 如图所示,在等量异种电荷连线的中垂线上取A、B、C、D四点,B、D两点关于O点对称,则关于各点场强的关系,下列说法中正确的是( )
如图所示,在等量异种电荷连线的中垂线上取A、B、C、D四点,B、D两点关于O点对称,则关于各点场强的关系,下列说法中正确的是( )| A. | EA>EB,EB=ED | B. | EA<EB<EC,EB=ED | ||
| C. | 四点场强方向不尽相同 | D. | EA<EB,EC与ED 大小关系无法确定 |
15.下列说法正确的是( )
| A. | 除了一些有机物质的大分子外,大多数分子大小的数量级为10-10cm | |
| B. | 当分子间距离增大时,分子间引力增大,分子间斥力减小 | |
| C. | 物体的内能与物体所含物质的多少、物体的温度和物体的体积都有关 | |
| D. | 水的饱和汽压随温度的升高而增大 | |
| E. | 热力学第二定律可以表述为:不可能从单一热源吸热,使之完全变成功,而不产生其他影响 |
 如图所示,一平直的传送带以速度v=2m/s匀速运行,传送带把A点处的零件运送到B点处,A、B两点之间相距L=10m,从A点把零件轻轻地放到传送带上,经过时间t=6s,送到B点,如果提高传送带的运动速率,零件能较快地传送到B点,要让零件用最短的时间从A点传送到B点处,说明并计算传送带的运动速率至少应多大?如果把求得的速率再提高一倍,则零件传送时间为多少?
如图所示,一平直的传送带以速度v=2m/s匀速运行,传送带把A点处的零件运送到B点处,A、B两点之间相距L=10m,从A点把零件轻轻地放到传送带上,经过时间t=6s,送到B点,如果提高传送带的运动速率,零件能较快地传送到B点,要让零件用最短的时间从A点传送到B点处,说明并计算传送带的运动速率至少应多大?如果把求得的速率再提高一倍,则零件传送时间为多少?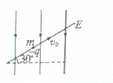 如图所示,一带电液滴质量为m,带电荷为-q,在竖直向下的匀强电场中刚好在与水平面成30°的直线上以速度v0向上做匀速直线运动,问:
如图所示,一带电液滴质量为m,带电荷为-q,在竖直向下的匀强电场中刚好在与水平面成30°的直线上以速度v0向上做匀速直线运动,问: