题目内容
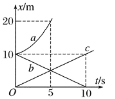
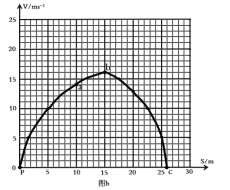
【题目】研究“蹦极”运动时，让运动员身上装好传感器，用以测量他在不同时刻下落的高度及速度。如图a所示，运动员及所携带的全部设备的总质量为60 kg，弹性绳原长为10m。运动员（可看做质点）从蹦极台（P点）自由下落，根据传感器测到的数据，得到如图b所示的速度－位移图象。已经测量得知当地的重力加速度g为9.80m/s2 。不计下落过程中的空气阻力。
(1)运动员下落过程中在什么位置动能最大？在该位置运动员受力有什么特点？
(2)运动员下落速度最大时，绳的弹性势能为多少?
(3)若运动员下落到最低点时，绳的弹性势能非常巧合地可以表示成
，式中k相当于弹性绳此刻的劲度系数，x是弹性绳此刻的形变量。求此刻运动员的加速度（最后结果保留2位小数）?
【答案】(1)15m；运动员受到向上的弹力等于重力 (2)1140J (3)
，方向竖直向上
【解析】
(1)由图b可知：下落15m时速度最大，动能最大。此位置运动员加速度为零，合外力为零。
由于空气阻力可忽略不计，运动过程中机械能守恒，所以运动员受到向上的弹力等于重力.
(2)由图b可知速度最大时下落的距离s=15m， 速度v1=16m/s，下落过程中只有重力与弹力做功，因此机械能守恒。则绳的弹性势能：
(3)由图b可知运动员到达最低点时s2=26m，根据机械能守恒定律，运动员所有的重力势能转化为弹性势能，因此此时的弹性势能
由牛顿第二定律可知：
当
时，带入解得：，方向竖直向上.
答：(1)运动员下落过程下落15m时动能最大；在该位置运动员受到向上的弹力等于重力.
(2)运动员下落速度最大时，绳的弹性势能为1440J.
(3)此刻运动员的加速度22.05m/s2,方向竖直向上.
练习册系列答案
相关题目
