题目内容
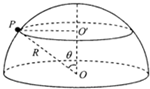（2008?四川）如图，一半径为R的光滑绝缘半球面开口向下，固定在水平面上．整个空间存在匀强磁场，磁感应强度方向竖直向下．一电荷量为q（q＞0）、质量为m的小球P在球面上做水平的匀速圆周运动，圆心为O′．球心O到该圆周上任一点的连线与竖直方向的夹角为θ（0＜θ＜| π | 2 |
分析：球P在球面上做水平的匀速圆周运动，需要正确地对其进行受力分析并结合向心力的公式，求出相应的结果．
解答：解：据题意，小球P在球面上做水平的匀速圆周运动，该圆周的圆心为O′．P受到向下的重力mg、球面对它沿OP方向的支持力N和磁场的洛仑兹力：f=qvB…①
式中v为小球运动的速率．洛仑兹力f的方向指向O′．根据牛顿第二定律：Ncosθ-mg=0…②
f-Nsinθ=m
…③
由①②③式得：v2-
v+
=0…④
由于v是实数，必须满足：△=(
)2-
≥0…⑤
由此得：B≥
…⑥
可见，为了使小球能够在该圆周上运动，磁感应强度大小的最小值为：Bmin=
…⑦
此时，带电小球做匀速圆周运动的速率为：v=
…⑧
由⑦⑧式得：v=
sinθ…⑨
答：磁感应强度大小的最小值
，小球P相应的速率
sinθ．
式中v为小球运动的速率．洛仑兹力f的方向指向O′．根据牛顿第二定律：Ncosθ-mg=0…②
f-Nsinθ=m
| v2 |
| Rsinθ |
由①②③式得：v2-
| qBRsinθ |
| m |
| qRsin2θ |
| cosθ |
由于v是实数，必须满足：△=(
| qBRsinθ |
| m |
| 4gRsin2θ |
| cosθ |
由此得：B≥
| 2m |
| q |
|
可见，为了使小球能够在该圆周上运动，磁感应强度大小的最小值为：Bmin=
| 2m |
| q |
|
此时，带电小球做匀速圆周运动的速率为：v=
| qBminRsinθ |
| 2m |
由⑦⑧式得：v=
|
答：磁感应强度大小的最小值
| 2m |
| q |
|
|
点评：该题中，正确地进行受力分析是解题的关键．
练习册系列答案
相关题目
（2008?四川）如图．地球赤道上的山丘e，近地资源卫星p和同步通信卫星q均在赤道平面上绕地心做匀速圆周运动．设e、p、q，的圆周运动速率分别为v1、v2、v3，向心加速度分别为a1、a2、a3，则（ ）
（2008?四川）如图，一理想变压器原线圈接入一交流电源，副线圈电路中R1、R2、R3和R4均为固定电阻，开关S是闭合的．
和
为理想电压表，读数分别为U1和U2；
、
和
为理想电流表，读数分别为I1、I2和I3．现断开S，U1数值不变，下列推断中正确的是（ ）
（2008?四川）如图，一束单色光射入一玻璃球体，入射角为60°．己知光线在玻璃球内经一次反射后，再次折射回到空气中时与入射光线平行．此玻璃的折射率为（ ）
（2008?四川）如图，在真空中一条竖直向下的电场线上有两点a和b．一带电质点在a处由静止释放后沿电场线向上运动，到达b点时速度恰好为零．则下面说法正确的是（ ）
（2008?四川）如图，一质量为m=1kg的木板静止在光滑水平地面上．开始时，木板右端与墙相距L=0.08m；质量为m=1kg 的小物块以初速度v0=2m/s 滑上木板左端．木板长度可保证物块在运动过程中不与墙接触．物块与木板之间的动摩擦因数为μ=0.1．木板与墙的碰撞是完全弹性的．取g=10m/s2，求