题目内容
12.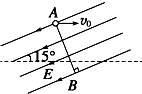 如图所示,处于真空中的匀强电场与水平方向成15°角,AB直线与匀强电场E垂直.在A点以大小为v0的初速度水平抛出一质量为m、电荷量为+q的小球,经时间t,小球下落一段距离过C点(图中未画出)时速度大小仍为v0.在小球由A点运动到C点的过程中,下列说法正确的是( )
如图所示,处于真空中的匀强电场与水平方向成15°角,AB直线与匀强电场E垂直.在A点以大小为v0的初速度水平抛出一质量为m、电荷量为+q的小球,经时间t,小球下落一段距离过C点(图中未画出)时速度大小仍为v0.在小球由A点运动到C点的过程中,下列说法正确的是( )| A. | C可能位于AB直线的左侧 | |
| B. | 小球的电势能增量大于$\frac{1}{2}$mg2t2 | |
| C. | 电场力对小球做功为零 | |
| D. | 若E=$\frac{mg}{q}$,则小球速度最小时,速度与水平方向成15°角 |
分析 小球由A点运动到C点的过程中,重力做正功,动能不变,由动能定理可判断出电场力做负功,机械能减小,C点的电势比A点电势高,可知C点位于AB直线的右侧,并利用类斜抛的合成与分解方法,依据合力方向速度为零,则球达到最高点,即速度最小,从而即可求解.
解答 解:A、小球的电势能增加,而小球带正电,则知C点的电势比A点电势高,故C点一定位于AB直线的右侧,故A错误;
B、小球具有机械能和电势能,总是守恒,小球的电势能增加,则知小球的机械能一定减小,小球具有机械能和电势能,总量守恒,小球的电势能增加,则知小球的机械能一定减小,小球的机械能的减少量即为竖直方向的重力势能的减少量mgh,由于电场力向左下方,重力竖直向下,将合力沿着水平和竖直方向正交分解,竖直方向的合力大于重力,故在竖直方向的分运动的加速度a大于g,竖直方向h=$\frac{1}{2}$at2>$\frac{1}{2}$gt2,即mgh>$\frac{1}{2}$mg2t2,.故B正确.
C、由题,小球由A点运动到C点的过程中,重力做正功,动能不变,由动能定理得知,电场力必定做负功,小球的电势能增加.故C错误.
D、由题意可知,当速度方向与球受到的合力方向垂直时,速度达到最小,由于E=$\frac{mg}{q}$,即电场力等于重力,那么合力与竖直方向夹角为37.5°,因此速度与水平方向成37.5°.故D错误.
故选:B.
点评 本题运用动能定理分析电场力做功正负,并分析电势能、机械能的变化.根据推论:正电荷在电势高处电势能大,分析C点的位置,并掌握类斜抛运动的处理规律,注意速度方向与合力方向垂直时,速度达到最小,是解D选项的关键.

练习册系列答案
相关题目
2.下列表述不符合物理史实的是( )
| A. | 伽利略提出了太阳系行星运动的第三大定律 | |
| B. | 牛顿提出了万有引力定律 | |
| C. | 卡文迪许首先测出了万有引力常量 | |
| D. | 爱因斯坦建立狭义相对论 |
3.关于生活中的圆周运动,下列说法正确的是( )
| A. | 转速很高的切割砂轮半径越大越好 | |
| B. | 在水平公路上转弯时汽车速度过大将做离心运动而造成事故 | |
| C. | 在修筑铁路时,转弯处铁轨的内轨要低于外轨是为了减轻火车轮缘与外轨的挤压 | |
| D. | 市内公共汽车转弯前提醒“车辆转弯,请拉好扶手”是防止站立的乘客转弯时向内侧倾倒 |
20.物体以速度v0水平抛出,若不计空气阻力,则当其竖直方向的位移与水平方向的位移相等时,以下说法中不正确的是( )
| A. | 竖直分速度为$\sqrt{2}$v0 | B. | 即时速度大小为$\sqrt{5}$v0 | ||
| C. | 运动的时间为$\frac{2{v}_{0}}{g}$ | D. | 运动的位移为$\frac{2\sqrt{2}{{v}_{0}}^{2}}{g}$ |
7.一物体自由下落,经时间t恰好落至地面,那么,在$\frac{t}{2}$时刻,物体的势能和动能之比为( )
| A. | 3:1 | B. | 1:3 | C. | 2:1 | D. | 1:2 |
17.一列简谐横波,在t=5.0s时的波形如图甲所示,图乙是这列波中质点P的振动图线,那么该波的传播速度和传播方向是( )


| A. | v=0.25 m/s,向右传播 | B. | v=0.50 m/s,向右传播 | ||
| C. | v=0.25 m/s,向左传播 | D. | v=0.50 m/s,向左传播 |
4. 质量为m的物体从倾角为30°的斜面上静止开始下滑s,物体与斜面之间的动摩擦因数μ=$\frac{\sqrt{3}}{4}$,下列说法中不正确的是( )
质量为m的物体从倾角为30°的斜面上静止开始下滑s,物体与斜面之间的动摩擦因数μ=$\frac{\sqrt{3}}{4}$,下列说法中不正确的是( )
 质量为m的物体从倾角为30°的斜面上静止开始下滑s,物体与斜面之间的动摩擦因数μ=$\frac{\sqrt{3}}{4}$,下列说法中不正确的是( )
质量为m的物体从倾角为30°的斜面上静止开始下滑s,物体与斜面之间的动摩擦因数μ=$\frac{\sqrt{3}}{4}$,下列说法中不正确的是( )| A. | 物体的动能增加$\frac{1}{8}$mgs | B. | 物体的重力势能减少$\frac{1}{8}$mgs | ||
| C. | 物体克服阻力所做的功为$\frac{3}{8}$mgs | D. | 物体的机械能减少$\frac{1}{2}$mgs |
5.(多选题)下列关于振动和波的说法中正确的是( )
| A. | 单摆在周期性外力作用下做受迫振动,其振动周期与单摆的摆长无关 | |
| B. | 变化的电场一定产生变化的磁场,变化的磁场一定产生变化的电场 | |
| C. | 当一列声波从空气中传入水中时波长一定会变短 | |
| D. | 麦克斯韦预言了电磁波的存在,赫兹通过实验证实 |
6.质量为m的汽车,启动后沿平直路面行驶,如果发动机功率恒为P,且行驶过程中受到的阻力大小一定,汽车速度能够达到的最大值为v,那么当汽车的车速为$\frac{v}{6}$时,汽车的瞬时加速度的大小为( )
| A. | $\frac{2P}{mv}$ | B. | $\frac{3P}{mv}$ | C. | $\frac{4P}{mv}$ | D. | $\frac{5P}{mv}$ |