题目内容
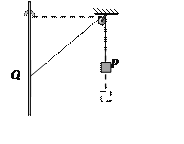
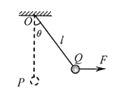
【题目】如图所示，一质量为m的小球，用长为L的轻绳悬挂于O点，初始时刻小球静止于P点。第一次小球在水平拉力F作用下，从P点缓慢地移动到Q点，此时轻绳与竖直方向夹角为θ，张力大小为T1；第二次在水平恒力F′作用下，从P点开始运动并恰好能到达Q点，至Q点时轻绳中的张力大小为T2，不计空气阻力，重力加速度为g，关于这两个过程，下列说法中正确的是( )
A. 第一个过程中，拉力F在逐渐变大，且最大值一定大于F′
B. 两个过程中，轻绳的张力均变大
C. 
， 
D. 第二个过程中，重力和水平恒力F′的合力的功率的变化是增大、减小、增大、减小
【答案】ACD
【解析】第一次小球在水平拉力F作用下，从P点缓慢地移动到Q点，则小球处于平衡状态，根据平衡条件得：F=mgtanθ，随着θ增大，F逐渐增大，第二次从P点开始运动并恰好能到达Q点，则到达Q点时速度为零，在此过程中，根据动能定理得：F′lsinθ=mgl（1-cosθ），解得：F′=mgtan
，因为θ＜90°，所以tan
＜mgtanθ，则F＞F′，第一次运动过程中，根据几何关系可知，绳子的拉力T=
，所以轻绳的张力变大，第二次由于重力和拉力都是恒力，可以把这两个力合成为新的“重力”，则第二次小球的运动可以等效于单摆运动，当绳子方向与重力和F′方向在同一直线上时，小球处于“最低点”，最低点的速度最大，此时绳子张力最大，所以第二次绳子张力先增大，后减小，故A正确，B错误；第一次运动到Q点时，受力平衡，根据几何关系可知， 
，第二次运动到Q点时，速度为零，则向心力为零，则绳子拉力T2=mgcosθ+F′sinθ=mgcosθ+
=mg，故C正确；第二个过程中，重力和水平恒力F′的合力是个恒力，在等效最低点时，合力方向与速度方向垂直，此时功率最小为零，到达Q点速度也为零，则第二个过程中，重力和水平恒力F′的合力的功率先增大，后减小，再增大，最后再减小为0，故D正确．故选ACD．
