题目内容
 如图所示,某空间有一竖直向下的匀强电场,电场强度E=1.0×102V/m,一块足够大的接地金属板水平放置在匀强电场中,在金属板的正上方高度h=0.80m的a处有一粒子源,盒内粒子以v0=2.0×102m/s的初速度向水平面以下的各个方向均匀放出质量为m=2.0×10-15kg,电荷量为q=+10-12C的带电粒子,粒子最终落在金属板b上.若不计粒子重力,求:(结果保留两位有效数字)
如图所示,某空间有一竖直向下的匀强电场,电场强度E=1.0×102V/m,一块足够大的接地金属板水平放置在匀强电场中,在金属板的正上方高度h=0.80m的a处有一粒子源,盒内粒子以v0=2.0×102m/s的初速度向水平面以下的各个方向均匀放出质量为m=2.0×10-15kg,电荷量为q=+10-12C的带电粒子,粒子最终落在金属板b上.若不计粒子重力,求:(结果保留两位有效数字)(1)粒子源所在处a点的电势;
(2)带电粒子打在金属板上时的动能;
(3)从粒子源射出的粒子打在金属板上的范围(所形成的面积).
分析:(1)金属板接地,电势为零,粒子源处a点的电势高于金属板的电势,由U=Eh求出粒子源与金属板间的电势差,即为a点的电势;
(2)粒子向金属板运动的过程中,只有电场力做功,根据动能定理求解粒子打在金属板上时的动能;
(3)粒子向各个方向向下运动,打金属板上形成一个圆形区域,当粒子初速度方向水平方向向左或右时,粒子做类平抛运动,打在圆形区域的边界上,水平位移等于圆的半径,根据牛顿第二定律和运动学公式,求解圆的半径,再求解面积.
(2)粒子向金属板运动的过程中,只有电场力做功,根据动能定理求解粒子打在金属板上时的动能;
(3)粒子向各个方向向下运动,打金属板上形成一个圆形区域,当粒子初速度方向水平方向向左或右时,粒子做类平抛运动,打在圆形区域的边界上,水平位移等于圆的半径,根据牛顿第二定律和运动学公式,求解圆的半径,再求解面积.
解答:解:(1)粒子源所在处a点的电势φa=Eh=80V
(2)由动能定理得
qEh=Ek-
m
得到EK=qEh+
m
=1.2×10-10J
(3)粒子源打在金属板上的范围是圆,设半径为R,
则 h=
at2=
?
?t2,R=v0t
解得R=v0
代入数据得:R=0.8
m
所以面积为:S=πR2=4m2
答:(1)粒子源所在处a点的电势为80V;
(2)带电粒子打在金属板上时的动能为1.2×10-10J;
(3)从粒子源射出的粒子打在金属板上所形成的面积为4m2.
(2)由动能定理得
qEh=Ek-
| 1 |
| 2 |
| v | 2 0 |
得到EK=qEh+
| 1 |
| 2 |
| v | 2 0 |
(3)粒子源打在金属板上的范围是圆,设半径为R,
则 h=
| 1 |
| 2 |
| 1 |
| 2 |
| qE |
| m |
解得R=v0
|
代入数据得:R=0.8
| 2 |
所以面积为:S=πR2=4m2
答:(1)粒子源所在处a点的电势为80V;
(2)带电粒子打在金属板上时的动能为1.2×10-10J;
(3)从粒子源射出的粒子打在金属板上所形成的面积为4m2.
点评:求解电势,往往先求出某点与零电势的电势差,再求解电势;本题实质是类平抛运动问题,采用运动的分解法进行处理,常规题.

练习册系列答案
相关题目
 如图所示,某空间有一竖直向下的匀强电场,电场强度E,一块足够大的接地金属板水平放置在匀强电场中,在金属板的正上方高度h的a处有一微粒源,盒内微粒以V0的初速度向水平面以下的各个方向均匀放出质量为m,电荷量为q的带正电微粒,粒子最终落在金属板b上.求:(要考虑微粒的重力,阻力不计)
如图所示,某空间有一竖直向下的匀强电场,电场强度E,一块足够大的接地金属板水平放置在匀强电场中,在金属板的正上方高度h的a处有一微粒源,盒内微粒以V0的初速度向水平面以下的各个方向均匀放出质量为m,电荷量为q的带正电微粒,粒子最终落在金属板b上.求:(要考虑微粒的重力,阻力不计)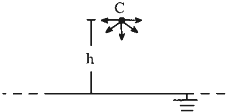 (2010?海南模拟)如图所示,某空间有一竖直向下的匀强电场,电场强度E=1.0×102V/m,一块足够大的接地金属板水平放置在匀强电场中,在金属板的正上方高度h=0.80m的C处有一粒子源,可在纸面内向水平线以下的各个方向均匀放出带电粒子,带电粒子的初速度
(2010?海南模拟)如图所示,某空间有一竖直向下的匀强电场,电场强度E=1.0×102V/m,一块足够大的接地金属板水平放置在匀强电场中,在金属板的正上方高度h=0.80m的C处有一粒子源,可在纸面内向水平线以下的各个方向均匀放出带电粒子,带电粒子的初速度