题目内容
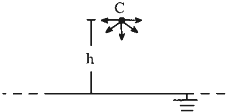 (2010?海南模拟)如图所示,某空间有一竖直向下的匀强电场,电场强度E=1.0×102V/m,一块足够大的接地金属板水平放置在匀强电场中,在金属板的正上方高度h=0.80m的C处有一粒子源,可在纸面内向水平线以下的各个方向均匀放出带电粒子,带电粒子的初速度v0=2.0×102m/s,质量为m=2.0×10-15kg,电荷量为q=+10-12C,粒子最终落在金属板上.若不计粒子重力,求:
(2010?海南模拟)如图所示,某空间有一竖直向下的匀强电场,电场强度E=1.0×102V/m,一块足够大的接地金属板水平放置在匀强电场中,在金属板的正上方高度h=0.80m的C处有一粒子源,可在纸面内向水平线以下的各个方向均匀放出带电粒子,带电粒子的初速度v0=2.0×102m/s,质量为m=2.0×10-15kg,电荷量为q=+10-12C,粒子最终落在金属板上.若不计粒子重力,求:(1)粒子源所在处C点的电势;
(2)带电粒子打在金属板上时的动能;
(3)若只将电场换为匀强磁场,磁场分布在半径为h,圆心在C点的圆形区域内,磁场方向垂直纸面向里,磁感应强度为B=0.5T,从粒子源射出的粒子打在金属板上的范围.(结果保留两位有效数字,
| 3 |
分析:(1)金属板接地,电势为零,粒子源处a点的电势高于金属板的电势,由U=Eh求出粒子源与金属板间的电势差,即为a点的电势;
(2)粒子向金属板运动的过程中,只有电场力做功,根据动能定理求解粒子打在金属板上时的动能;
(3)粒子向各个方向向下运动,根据左手定则可以判断出粒子在磁场中向右偏转,所以向左方向入射的粒子范围比较小,而向右入射的粒子可以飞到无穷远处,根据洛伦兹力提供向心力,可以求出粒子在磁场中运动的半径和偏转角,然后求出范围.
(2)粒子向金属板运动的过程中,只有电场力做功,根据动能定理求解粒子打在金属板上时的动能;
(3)粒子向各个方向向下运动,根据左手定则可以判断出粒子在磁场中向右偏转,所以向左方向入射的粒子范围比较小,而向右入射的粒子可以飞到无穷远处,根据洛伦兹力提供向心力,可以求出粒子在磁场中运动的半径和偏转角,然后求出范围.
解答:解:(1)依据题意,设C点的电势为UC:UC=Eh=80V
(2)根据动能定理,设打到金属板时的动能为EK :qU=Ek-Ek0
Ek0=
m
得Ek=1.2×10-10J
(3)如图建立xoy平面坐标系,在x<0区域内从粒子源沿水平方向飞出的带电粒子打在金属板上的距离最远.粒子磁场中做匀速圆周运动从M点飞出,

圆周半径为:r=
=0.8m
可知:飞出磁场时的速度方向与水平向成60°角,△COM为等边三角形,飞出磁场后做匀速直线运动打在金属板上由几何关系可知:
ON=rsin60°+
r?tan30°=
m
x>0区域内从磁场飞出的带电粒子速度偏转的方向向右,可以打在金属板的无穷远处.
所以打在金属板上范围为:-
≤x<∞
答:(1)粒子源所在处C点的电势为80V;
(2)带电粒子打在金属板上时的动能为1.2×10-10J;
(3)若只将电场换为匀强磁场,从粒子源射出的粒子打在金属板上的范围是-
≤x<∞.
(2)根据动能定理,设打到金属板时的动能为EK :qU=Ek-Ek0
Ek0=
| 1 |
| 2 |
| v | 2 0 |
得Ek=1.2×10-10J
(3)如图建立xoy平面坐标系,在x<0区域内从粒子源沿水平方向飞出的带电粒子打在金属板上的距离最远.粒子磁场中做匀速圆周运动从M点飞出,

圆周半径为:r=
| mv0 |
| Bq |
可知:飞出磁场时的速度方向与水平向成60°角,△COM为等边三角形,飞出磁场后做匀速直线运动打在金属板上由几何关系可知:
ON=rsin60°+
| 1 |
| 2 |
8
| ||
| 15 |
x>0区域内从磁场飞出的带电粒子速度偏转的方向向右,可以打在金属板的无穷远处.
所以打在金属板上范围为:-
8
| ||
| 15 |
答:(1)粒子源所在处C点的电势为80V;
(2)带电粒子打在金属板上时的动能为1.2×10-10J;
(3)若只将电场换为匀强磁场,从粒子源射出的粒子打在金属板上的范围是-
8
| ||
| 15 |
点评:求解电势,往往先求出某点与零电势的电势差,再求解电势;本题实质是类平抛运动问题,采用运动的分解法进行处理,常规题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
 (2010?海南模拟)如图 是某电磁冲击钻的原理图,若突然发现钻头M向右运动,则可能是( )
(2010?海南模拟)如图 是某电磁冲击钻的原理图,若突然发现钻头M向右运动,则可能是( ) (2010?海南模拟)如图所示,小球从A点以初速度v0沿粗糙斜面向上运动,到达最高点B后返回A,C为AB的中点.下列说法中正确的是( )
(2010?海南模拟)如图所示,小球从A点以初速度v0沿粗糙斜面向上运动,到达最高点B后返回A,C为AB的中点.下列说法中正确的是( )
 (2010?海南模拟)一质量为0.5kg的滑块以6m/s的初速度冲上一倾角为30°足够长的斜面,某同学利用DIS实验系统测出了滑块冲上斜面过程中多个时刻的瞬时速度,如图所示为通过计算机绘制出的滑块上滑过程的v-t图.求:(g取10m/s.)
(2010?海南模拟)一质量为0.5kg的滑块以6m/s的初速度冲上一倾角为30°足够长的斜面,某同学利用DIS实验系统测出了滑块冲上斜面过程中多个时刻的瞬时速度,如图所示为通过计算机绘制出的滑块上滑过程的v-t图.求:(g取10m/s.) (2010?海南模拟)介子由两个夸克构成,而夸克之间的相互作用相当复杂.研究介子可通过用高能电子与之作非弹性碰撞来进行.由于碰撞过程难于分析,为掌握其主要内涵,人们发展了一种简化了的“分粒子”模型.其主要内容为:电子只和介子的某部分(比如其中一个夸克)作弹性碰撞.碰撞后的夸克再经过介子内的相互作用把能量和动量传给整个介子.
(2010?海南模拟)介子由两个夸克构成,而夸克之间的相互作用相当复杂.研究介子可通过用高能电子与之作非弹性碰撞来进行.由于碰撞过程难于分析,为掌握其主要内涵,人们发展了一种简化了的“分粒子”模型.其主要内容为:电子只和介子的某部分(比如其中一个夸克)作弹性碰撞.碰撞后的夸克再经过介子内的相互作用把能量和动量传给整个介子.