题目内容
 如图所示,两足够长平行光滑的水平金属导轨MN、PQ相距为l=0.5m,两轨道与等宽的平行金属导轨MA、PC相连,A、C之间接有电阻R=0.3Ω.倾斜轨道面与水平面所成夹角为θ=37°,倾斜轨道处有磁感应强度为B1=0.1T的匀强磁场垂直MA、CP导轨平面向上.在水平轨道MNPQ、处有磁感应强度为B2=0.8T竖直向上的匀强磁场.今有一质量为m=0.2kg、电阻为r=0.2Ω的金属棒从倾斜轨道上距离下端为s0=1.0m处由静止释放(金属棒始终与轨道垂直),已知金属棒与倾斜轨道间动摩擦因数为μ=0.5,金属棒到达倾斜轨道底端前已匀速运动,通过底端进入水平轨道时速度大小不改变,已知金属棒在水平轨道运动的过程中,通过电阻R的电荷量q=0.2c(g取10m/s2,sin37°=0.6,cos37°=0.8).求:
如图所示,两足够长平行光滑的水平金属导轨MN、PQ相距为l=0.5m,两轨道与等宽的平行金属导轨MA、PC相连,A、C之间接有电阻R=0.3Ω.倾斜轨道面与水平面所成夹角为θ=37°,倾斜轨道处有磁感应强度为B1=0.1T的匀强磁场垂直MA、CP导轨平面向上.在水平轨道MNPQ、处有磁感应强度为B2=0.8T竖直向上的匀强磁场.今有一质量为m=0.2kg、电阻为r=0.2Ω的金属棒从倾斜轨道上距离下端为s0=1.0m处由静止释放(金属棒始终与轨道垂直),已知金属棒与倾斜轨道间动摩擦因数为μ=0.5,金属棒到达倾斜轨道底端前已匀速运动,通过底端进入水平轨道时速度大小不改变,已知金属棒在水平轨道运动的过程中,通过电阻R的电荷量q=0.2c(g取10m/s2,sin37°=0.6,cos37°=0.8).求:
(1)金属棒在运动过程中的最大速度.
(2)金属棒在水平轨道上运动的距离.
(3)整个过程中电阻R上产生的热量.
解:(1)当金属棒匀速下滑时速度最大,设最大速度为vm
F安=BIL
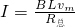
得mgsinθ=
解得vm=0.8m/s
故金属棒在运动过程中的最大速度为0.8m/s.
(2)金属棒在水平轨道运动的过程中,做减速运动直到停止,根据法拉第电磁感应定律得:
 ,
,
又
所以 ,
,
△Φ=B△S=BLx
解得:x-0.5m
故金属棒在水平轨道上运动的距离为0.5m.
(3)由能量守恒知,放出的总电热为
Q=mgs0sinθ-μmgs0cosθ
电阻R上产生的热量
 =0.24J
=0.24J
故整个过程中电阻R上产生的热量为0.24J.
分析:(1)当金属棒在下滑过程中,合外力为零时,速度最大,根据平衡求出金属棒的最大速度.
(2)抓住在水平轨道运动时通过电阻R的电荷量q=0.2c,结合法拉第电磁感应定律求出平均感应电流,根据q=It求出金属棒在水平轨道上运动的距离.
(3)金属棒的初动能为零,末动能为零,在整个运动的过程中,重力势能减小,知重力势能的减小量等于摩擦产生的热量和在整个电路中产生的热量之和,根据能量守恒求出整个电路产生的热量,从而得出电阻R上产生的热量.
点评:本题是力学和电磁学的综合题,综合运用了电磁感应定律、能量守恒定律以及共点力平衡问题,要注意第(3)问中求的是电阻R上产生的热量,不是整个电路上产生的热量.
F安=BIL
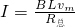
得mgsinθ=

解得vm=0.8m/s
故金属棒在运动过程中的最大速度为0.8m/s.
(2)金属棒在水平轨道运动的过程中,做减速运动直到停止,根据法拉第电磁感应定律得:
 ,
,又

所以
 ,
,△Φ=B△S=BLx
解得:x-0.5m
故金属棒在水平轨道上运动的距离为0.5m.
(3)由能量守恒知,放出的总电热为
Q=mgs0sinθ-μmgs0cosθ
电阻R上产生的热量
 =0.24J
=0.24J故整个过程中电阻R上产生的热量为0.24J.
分析:(1)当金属棒在下滑过程中,合外力为零时,速度最大,根据平衡求出金属棒的最大速度.
(2)抓住在水平轨道运动时通过电阻R的电荷量q=0.2c,结合法拉第电磁感应定律求出平均感应电流,根据q=It求出金属棒在水平轨道上运动的距离.
(3)金属棒的初动能为零,末动能为零,在整个运动的过程中,重力势能减小,知重力势能的减小量等于摩擦产生的热量和在整个电路中产生的热量之和,根据能量守恒求出整个电路产生的热量,从而得出电阻R上产生的热量.
点评:本题是力学和电磁学的综合题,综合运用了电磁感应定律、能量守恒定律以及共点力平衡问题,要注意第(3)问中求的是电阻R上产生的热量,不是整个电路上产生的热量.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
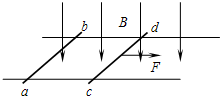 如图所示,两足够长平行金属导轨固定在水平面上,匀强磁场方向垂直导轨平面向下,金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动,两金属棒ab、cd的质量之比为2:1,用一沿导轨方向的恒力F水平向右拉金属棒cd,经过足够长时间以后( )
如图所示,两足够长平行金属导轨固定在水平面上,匀强磁场方向垂直导轨平面向下,金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动,两金属棒ab、cd的质量之比为2:1,用一沿导轨方向的恒力F水平向右拉金属棒cd,经过足够长时间以后( )
 如图所示,两足够长平行金属导轨固定在水平面上,匀强磁场方向垂直导轨平面向下,金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动,两金属棒ab、cd的质量之比为2:1,用一沿导轨方向的恒力F水平向右拉金属棒cd,经过足够长时间以后( )
如图所示,两足够长平行金属导轨固定在水平面上,匀强磁场方向垂直导轨平面向下,金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动,两金属棒ab、cd的质量之比为2:1,用一沿导轨方向的恒力F水平向右拉金属棒cd,经过足够长时间以后( )
 如图所示,两足够长平行金属导轨固定在水平面上,匀强磁场方向垂直导轨平面向下,金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动,两金属棒ab、cd的质量之比为2:1,用一沿导轨方向的恒力F水平向右拉金属棒cd,经过足够长时间以后( )
如图所示,两足够长平行金属导轨固定在水平面上,匀强磁场方向垂直导轨平面向下,金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动,两金属棒ab、cd的质量之比为2:1,用一沿导轨方向的恒力F水平向右拉金属棒cd,经过足够长时间以后( )
 如图所示,两足够长平行金属导轨固定在水平面上,匀强磁场方向垂直导轨平面向下,金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动,两金属棒ab、cd的质量之比为2:1,用一沿导轨方向的恒力F水平向右拉金属棒cd,经过足够长时间以后( )
如图所示,两足够长平行金属导轨固定在水平面上,匀强磁场方向垂直导轨平面向下,金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动,两金属棒ab、cd的质量之比为2:1,用一沿导轨方向的恒力F水平向右拉金属棒cd,经过足够长时间以后( )