Question

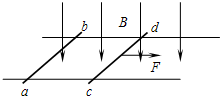如图所示，两足够长平行金属导轨固定在水平面上，匀强磁场方向垂直导轨平面向下，金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动，两金属棒ab、cd的质量之比为2：1，用一沿导轨方向的恒力F水平向右拉金属棒cd，经过足够长时间以后（　　）

• A、金属棒ab、cd都做匀速运动
• B、金属棒ab上的电流方向是由b向a
• C、金属棒cd所受安培力的大小等于

  2F

  3

• D、两金属棒间距离保持不变

Answer 1

分析：运用排除法分析AD两项：若金属棒ab做匀速运动，所受的安培力为零，ab中电流为零，则知cd中电流也为零，而cd还受到F作用，cd将做匀加速运动．若两金属棒间距离保持不变，同理可知，cd将做匀加速运动，两棒间距离将增大．由此分析可知，两棒都做匀加速运动，加速度相同，cd的速度大于ab的速度，由楞次定律分析感应电流方向，由牛顿第二定律求出加速度，再对cd研究，求出安培力的大小．

解答：解：A、D若金属棒ab做匀速运动，所受的安培力为零，ab中电流为零，则cd中电流也为零，cd不按安培力，而cd还受到F作用，cd将做匀加速运动．故A错误．若两金属棒间距离保持不变，回路的磁通量不变，没有感应电流产生，两棒都不受安培力，则cd将做匀加速运动，两者距离将增大．故AD均错误．
B、C由上分析得知，当两棒的运动稳定时，两棒速度之差一定，回路中产生的感应电流一定，两棒所受的安培力都保持不变，一起以相同的加速度做匀加速运动，由于两者距离不断增大，穿过回路的磁通量增大，由楞次定律判断可知，金属棒ab上的电流方向是由b向a．设cd棒的质量为m，则根据牛顿第二定律得：
   对整体：F=3ma
   对cd棒：F-F_A=ma
解得，F_A=

2

3

F．故BC正确．
故选BC

点评：本题的解题关键是分析两棒的运动情况，本题回路中的感应电动势为E=BL△v，△v是两棒速度之差．