题目内容
【题目】如图所示,某游乐园的一个摩天轮的半径为10米,轮子的底部到地面的距离为2米,该摩天轮沿逆时针方向旋转,且每20分钟旋转一圈,当摩天轮上某人经过点![]() (到地面的高度为17米)时开始计时,
(到地面的高度为17米)时开始计时,![]() .
.
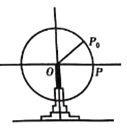
(1)求此人转动5分钟后相对于地面的高度;
(2)当摩天轮上此人经过点![]() 时,
时,![]() ,求
,求![]() .
.
【答案】(1)![]() 米;(2)
米;(2)![]() .
.
【解析】
(1)易得此人转动后相对于地面的高度满足![]() 的结构.故以
的结构.故以![]() 为坐标原点,以
为坐标原点,以![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系,再根据题意与三角函数的性质,根据周期求解
轴,建立平面直角坐标系,再根据题意与三角函数的性质,根据周期求解![]() ,再根据初十位置求解
,再根据初十位置求解![]() 即可.
即可.
(2) 由(1)可知,![]() ,再根据
,再根据![]() 化简可得
化简可得
![]() ,进而利用
,进而利用![]() 求解即可.
求解即可.
(1)以![]() 为坐标原点,以
为坐标原点,以![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系,
轴,建立平面直角坐标系,
此人在摩天轮上每分钟转过的角为![]() ,
,
所以![]() 分钟时,此人的纵坐标为
分钟时,此人的纵坐标为![]() ,
,
所以![]() 分钟时,此人相对于地面的高度为
分钟时,此人相对于地面的高度为![]() .
.
当![]() 时,
时,![]() 则
则![]() 所以
所以![]() ,
,
则![]() .
.
所以5分钟后的高度为![]() (米).
(米).
(2)由(1)可知,![]() ,
,
则![]() ,
,
即![]() ,
,
所以![]() ,所以
,所以![]() .
.
又因为![]() 所以
所以![]() ,
,
故![]()
![]() .
.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
【题目】弹簧振子的振动是简谐振动.某个弹簧振子在完成一次全振动的过程中,时间t(单位:s)与位移y(单位:mm)之间的对应数据记录如下表:
t | 0.00 | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 | 0.50 | 0.55 | 0.60 |
y |
|
|
|
| 10.0 | 17.7 | 20.0 | 17.7 | 10.0 |
|
|
|
|
(1)试根据这些数据确定这个振子的位移关于时间的函数解析式;
(2)画出该函数在![]() 的函数图象;
的函数图象;
(3)在整个振动过程中,求位移为10mm时![]() 的取值集合.
的取值集合.