题目内容
13. 如图所示,在光滑的水平面上有一质量为25kg的小车B,上面放一个质量为15kg的物体,物体与车间的滑动摩擦系数为0.2.另有一辆质量为20kg的小车A以3m/s的速度向前运动.A与B相碰后连在一起,物体一直在B车上滑动.求:
如图所示,在光滑的水平面上有一质量为25kg的小车B,上面放一个质量为15kg的物体,物体与车间的滑动摩擦系数为0.2.另有一辆质量为20kg的小车A以3m/s的速度向前运动.A与B相碰后连在一起,物体一直在B车上滑动.求:(1)当车与物体以相同的速度前进时的速度.
(2)物体在B车上滑动的距离.
分析 (1)对于小车A、B和B车上的物体组成的系统,从A、B接触到车与物体以相同的速度前进的整个过程中,系统所受合外力为零,系统的动量守恒,根据动量守恒定律列式,即可求得.
(2)选取小车A、B组成的系统为研究对象,在它们相碰的短暂过程中,系统所受合外力为零,动量守恒,列式可求出碰后的共同速度,再对小车A、B和B车上的物体组成的系统为研究对象,根据动能定理或能量守恒定律求解物体在B车上滑动的距离.
解答 解:(1)选取小车A、B和B车上的物体组成的系统为研究对象,从A、B接触到车与物体以相同的速度前进的整个过程中,
系统所受合外力为零,系统动量守恒,以向右为正方向,根据动量守恒定律有:mAv0=(mA+mB+mC)v2
代入数据,可解得:v2=1m/s,即小车与物体以1m/s的速度前进.
(2)选取小车A、B组成的系统为研究对象,在它们相碰的短暂过程中,系统所受合外力为零,
动量守恒,以向右为正方向,由动量守恒定律得:mAv0=(mA+mB)v1,解得:v1=$\frac{4}{3}$m/s,
再选取小车A、B和B车上的物体组成的系统为研究对象,从A、B接触到车与物体以相同的速度前进的整个过程中,
根据动能定理有:-μmCgs=$\frac{1}{2}$(mA+mB+mC)v22-$\frac{1}{2}$(mA+mB)v12,解得:s=$\frac{1}{3}$m=0.33m;
答:(1)当车与物体以相同的速度前进时的速度是1m/s.
(2)物体在B车上滑动的距离是0.33m.
点评 本题分析物体的运动情况是解题的基础,关键要能运用动量守恒和动能定理结合进行求解,要注意选择研究过程和对象.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
10.在“测定直流电动机的效率”实验中,用如图(a)所示的电路测定一个额定电压为6V、额定功率为3W的直流电动机的机械效率.
(1)请根据图(a)完成图(b)中的实物图;
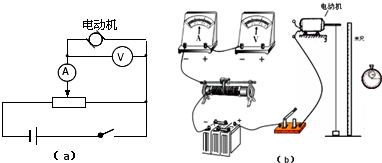
(2)实验中保持电动机两端电压U恒为6V,重物每次匀速上升的高度h均为1.5m,所测物理量及测量结果如下表所示:
计算电动机效率η的表达式为$η=\frac{mgh}{UIt}×100%$(用题目中的符号表示),第1次实验中电动机的工作效率为71.4%.(保留三位有效数字)
(3)在第5次实验中,电动机的输出功率是0;可估算出电动机线圈的电阻为2.4Ω.
(1)请根据图(a)完成图(b)中的实物图;

(2)实验中保持电动机两端电压U恒为6V,重物每次匀速上升的高度h均为1.5m,所测物理量及测量结果如下表所示:
| 实验次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 电动机的电流I/A | 0.2 | 0.4 | 0.6 | 0.8 | 2.5 | 2.5 |
| 所提重物的重力Mg/N | 0.8 | 2.0 | 4.0 | 6.0 | 6.5 | 7.0 |
| 重物上升时间t/s | 1.4 | 1.65 | 2.1 | 2.7 | ∞ | ∞ |
(3)在第5次实验中,电动机的输出功率是0;可估算出电动机线圈的电阻为2.4Ω.
4.某带电粒子仅在电场力作用下由A点运动到B点,运动轨迹如图所示,可以判定( )


| A. | 粒子在A点的加速度大于它在B点的加速度 | |
| B. | 粒子在A点的动能小于它在B点的动能 | |
| C. | 粒子带负电荷 | |
| D. | A点电势比B点电势低 |
1. 如图所示,地面上某个空间区域存在这样的电场,水平虚线上方为场强E1,方向竖直向下的匀强电场;虚线下方为场强E2,方向竖直向上的匀强电场.一个质量m,带电+q的小球从上方电场的A点由静止释放,结果刚好到达下方电场中与A关于虚线对称的B点,则下列结论正确的是( )
如图所示,地面上某个空间区域存在这样的电场,水平虚线上方为场强E1,方向竖直向下的匀强电场;虚线下方为场强E2,方向竖直向上的匀强电场.一个质量m,带电+q的小球从上方电场的A点由静止释放,结果刚好到达下方电场中与A关于虚线对称的B点,则下列结论正确的是( )
 如图所示,地面上某个空间区域存在这样的电场,水平虚线上方为场强E1,方向竖直向下的匀强电场;虚线下方为场强E2,方向竖直向上的匀强电场.一个质量m,带电+q的小球从上方电场的A点由静止释放,结果刚好到达下方电场中与A关于虚线对称的B点,则下列结论正确的是( )
如图所示,地面上某个空间区域存在这样的电场,水平虚线上方为场强E1,方向竖直向下的匀强电场;虚线下方为场强E2,方向竖直向上的匀强电场.一个质量m,带电+q的小球从上方电场的A点由静止释放,结果刚好到达下方电场中与A关于虚线对称的B点,则下列结论正确的是( )| A. | 若AB高度差为h,则UAB=-$\frac{mgh}{q}$ | |
| B. | 带电小球在AB两点电势能相等 | |
| C. | 在虚线上下方的电场中,带电小球运动的加速度相同 | |
| D. | 两电场强度大小关系满足E2=2E1 |
18.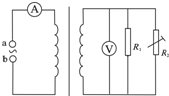 如图所示,理想变压器原、副线圈的匝数比为1:10,接线柱a、b接在电压为u=10$\sqrt{2}$sin100πtV的正弦交流电源上,R1为定值电阻,其阻值为100Ω,R2为用半导体材料制成的热敏电阻(阻值随温度升高而减小).下列说法中正确的是( )
如图所示,理想变压器原、副线圈的匝数比为1:10,接线柱a、b接在电压为u=10$\sqrt{2}$sin100πtV的正弦交流电源上,R1为定值电阻,其阻值为100Ω,R2为用半导体材料制成的热敏电阻(阻值随温度升高而减小).下列说法中正确的是( )
 如图所示,理想变压器原、副线圈的匝数比为1:10,接线柱a、b接在电压为u=10$\sqrt{2}$sin100πtV的正弦交流电源上,R1为定值电阻,其阻值为100Ω,R2为用半导体材料制成的热敏电阻(阻值随温度升高而减小).下列说法中正确的是( )
如图所示,理想变压器原、副线圈的匝数比为1:10,接线柱a、b接在电压为u=10$\sqrt{2}$sin100πtV的正弦交流电源上,R1为定值电阻,其阻值为100Ω,R2为用半导体材料制成的热敏电阻(阻值随温度升高而减小).下列说法中正确的是( )| A. | t=$\frac{1}{600}$ s时,a、b两点间电压的瞬时值为5$\sqrt{2}$V | |
| B. | t=$\frac{1}{600}$ s时,电压表的读数为50$\sqrt{2}$V | |
| C. | 在1分钟内电阻R1上产生的热量为6000J | |
| D. | 当R2的温度升高时,电压表示数变大,电流表示数变大 |
5.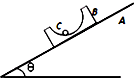 如图,小球C置于光滑的半球形凹槽B内,B放在长木板A上,整个装置处于静止状态,在缓慢减小木板的倾角θ过程中,下列说法正确的是( )
如图,小球C置于光滑的半球形凹槽B内,B放在长木板A上,整个装置处于静止状态,在缓慢减小木板的倾角θ过程中,下列说法正确的是( )
 如图,小球C置于光滑的半球形凹槽B内,B放在长木板A上,整个装置处于静止状态,在缓慢减小木板的倾角θ过程中,下列说法正确的是( )
如图,小球C置于光滑的半球形凹槽B内,B放在长木板A上,整个装置处于静止状态,在缓慢减小木板的倾角θ过程中,下列说法正确的是( )| A. | C对B的压力逐渐变大 | B. | C受到三个力的作用 | ||
| C. | B受到的摩擦力逐渐减小 | D. | A受到的压力逐渐减小 |
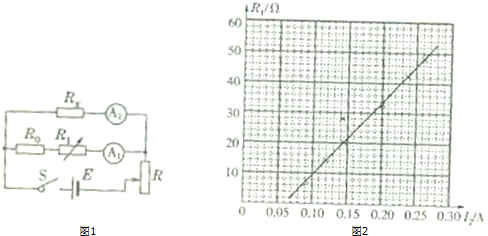

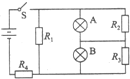 如图所示电路,开关S合上后,灯泡A、B均正常发光.当电路中某元件发生断路故障后,灯泡A变亮,灯泡B变暗.由此可知,发生断路的元件是( )
如图所示电路,开关S合上后,灯泡A、B均正常发光.当电路中某元件发生断路故障后,灯泡A变亮,灯泡B变暗.由此可知,发生断路的元件是( )