题目内容
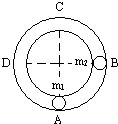
如图所示,在水平桌面上固定着一个光滑圆轨道,在轨道的B点静止着一个质量为m2的弹性小球乙,另一个质量为m1的弹性小球甲以初速v0运动,与乙球发生第一次碰撞后,恰在C点发生第二次碰撞.则甲、乙两球的质量之比m1:m2可能等于( )
| A.3:5 | B.1:9 | C.1:7 | D.2:3 |

设碰撞后m1、m2的速度分别为v1、v2.由题分析得到,m1碰后必然反向.
第一种情况:m1小球由A到B撞m2过程:
以v0方向为正,由动量守恒定律得:
m1v0=m2v2-m1v1…①
因为恰在C点发生第二次碰撞,在相同时间内,线速度大小与路程成正比,则有:
3v2=v1…②
且m1、m2为弹性球发生弹性碰撞,由机械能守恒得:
m1v02=
m1v12+
m2v22…③
将②代人①③得:
m1(v0+3v2)=m2v2
m1(v02-9v22)=m2v22
两式相除得v0=4v2
再代入①解得m1:m2=1:7
第二种情况:m1小球由A到D到C再到B撞m2过程:
以v0方向为正,由动量守恒定律得:
m1v0=m2v2-m1v1…①
因为恰在C点发生第二次碰撞,故有:
v2=3v1…②
且m1、m2为弹性球发生弹性碰撞,由机械能守恒得:
m1v02=
m1v12+
m2v22…③
解得:m1:m2=3:5
故选AC
第一种情况:m1小球由A到B撞m2过程:
以v0方向为正,由动量守恒定律得:
m1v0=m2v2-m1v1…①
因为恰在C点发生第二次碰撞,在相同时间内,线速度大小与路程成正比,则有:
3v2=v1…②
且m1、m2为弹性球发生弹性碰撞,由机械能守恒得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
将②代人①③得:
m1(v0+3v2)=m2v2
m1(v02-9v22)=m2v22
两式相除得v0=4v2
再代入①解得m1:m2=1:7
第二种情况:m1小球由A到D到C再到B撞m2过程:
以v0方向为正,由动量守恒定律得:
m1v0=m2v2-m1v1…①
因为恰在C点发生第二次碰撞,故有:
v2=3v1…②
且m1、m2为弹性球发生弹性碰撞,由机械能守恒得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:m1:m2=3:5
故选AC

练习册系列答案
 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 如图所示,在水平桌面的右边角处有一轻质光滑的定滑轮K,一条不可伸长的轻绳绕过K分别与物块A、B相连,A、B的质量分别为mA、mB,开始时系统处于静止状态,现用一竖直向下的恒力FY拉物块B,使物块A向右滑动.已知当B下降距离h时,A的速度为v,求物块A与桌面间地动摩擦因数.
如图所示,在水平桌面的右边角处有一轻质光滑的定滑轮K,一条不可伸长的轻绳绕过K分别与物块A、B相连,A、B的质量分别为mA、mB,开始时系统处于静止状态,现用一竖直向下的恒力FY拉物块B,使物块A向右滑动.已知当B下降距离h时,A的速度为v,求物块A与桌面间地动摩擦因数. 某同学设计了一个简易研究平抛运动特点的实验,装置如图所示,在水平桌面上放置一个斜面,每次让钢球从斜面上的同一位置滚下,离开桌边后做平抛运动.在钢球抛出后经过的地方水平放置一块木板(用来调节木板高度的支架在图中未画出),木板上放一张白纸,白纸上面有复写纸以记录钢球的落点.桌子边缘钢球经过的地方悬挂一条铅重锤.
某同学设计了一个简易研究平抛运动特点的实验,装置如图所示,在水平桌面上放置一个斜面,每次让钢球从斜面上的同一位置滚下,离开桌边后做平抛运动.在钢球抛出后经过的地方水平放置一块木板(用来调节木板高度的支架在图中未画出),木板上放一张白纸,白纸上面有复写纸以记录钢球的落点.桌子边缘钢球经过的地方悬挂一条铅重锤. 如图所示,在水平桌面上放一个重GA=20N的木块A,A与桌面间的动摩擦因数μ1=0.1,在A上放有重GB=10N的木块B,B与A接触面间的动摩擦因数μ2=0.4,求:
如图所示,在水平桌面上放一个重GA=20N的木块A,A与桌面间的动摩擦因数μ1=0.1,在A上放有重GB=10N的木块B,B与A接触面间的动摩擦因数μ2=0.4,求: 某同学设计了一个探究平抛运动特点的实验装置,如图所示:在水平桌面上放置一个斜面,让钢球从斜面上滚下,滚过桌面后钢球便做平抛运动在钢球抛出后经过的地方,水平放置一块木板(还有一个用来调节木板高度的支架,图中未画)木板上放一张白纸,白纸上有复写纸,这样便能记录钢球在白纸上的落点,桌子边缘钢球经过的地方挂一条铅垂线.
某同学设计了一个探究平抛运动特点的实验装置,如图所示:在水平桌面上放置一个斜面,让钢球从斜面上滚下,滚过桌面后钢球便做平抛运动在钢球抛出后经过的地方,水平放置一块木板(还有一个用来调节木板高度的支架,图中未画)木板上放一张白纸,白纸上有复写纸,这样便能记录钢球在白纸上的落点,桌子边缘钢球经过的地方挂一条铅垂线. 如图所示,在水平桌面上做匀速运动的两个小球,质量分别为m1和m2,沿着同一直线向相同的方向运动,速度分别为V1和V2,当第二个小球追上第一个小球时两球相碰,碰后的速度分别为V1′和V2′,试根据牛顿运动定律和运动学公式证明两球碰撞前的动量之和等于碰撞后的动量之和.
如图所示,在水平桌面上做匀速运动的两个小球,质量分别为m1和m2,沿着同一直线向相同的方向运动,速度分别为V1和V2,当第二个小球追上第一个小球时两球相碰,碰后的速度分别为V1′和V2′,试根据牛顿运动定律和运动学公式证明两球碰撞前的动量之和等于碰撞后的动量之和.