题目内容
如图所示，三个质量均为
的滑块
、
、
置于光滑水平面上.水平面右端与水平传送带之间无缝隙连接，传送带长度
，皮带轮沿顺时针方向转动，带动皮带以恒定速率
匀速传动．传送带右下方有一光滑圆弧固定轨道，其半径
，直径
竖直，
.开始时滑块、之间连接有（注：弹簧与滑块无栓接）一被压缩得不能再压缩的轻弹簧，弹簧被锁定并处于静止状态. 滑块以初速度
沿、连线方向向运动，与碰撞后粘合在一起，碰撞时间极短，此时连接、的弹簧突然解除锁定，弹簧伸展，从而使与、分离. 滑块脱离弹簧后以速度
滑上传送带，并从右端水平飞出后，由
点沿圆弧切线落入圆轨道，已知滑块与传送带之间的动摩擦因数
，重力加速度
取
．（滑块、、视为质点）求：
（1）滑块从传送带右端滑出时的速度大小.
（2）判断滑块能否沿光滑圆轨道到达最高点
，若能，求出滑块对圆轨道点的压力大小.若不能，请说明理由？
（3）弹簧最初的弹性势能
.
 |
解：（1）滑块滑上传送带有：
------------------------------------------------------- （1分）
-------------------------------------------------------------- （1分）
------------------------------------------------------------------（1分）
------------------------------------------------------------------ （1分）
所以，滑块先加速后匀速
-----------------------------------------------------------------------（1分）
（2）在点有：
--------------------------------------------（1分）
由点到点有：
-------------------（1分）
------------------------------------------（1分）
通过点满足
即
-----------------------------（1分）
因为
, 所以能通过点---------------------------------（1分）
在点有：
-------------------------------------------------（1分）
----------------------------------------------------------（1分）
（3）碰有：
--------------------------------------------------（2分）
与分离有:
-----------------------------------------（2分）
-------------------------------------------（2分）
--------------------------------------------------------------------------------（2分）
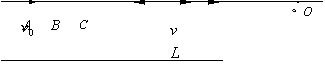
如图所示，三个质量均为m的弹性小球用两根长均为L的轻绳连成一条直线而静止在光滑水平面上．现给中间的小球B一个水平初速度v0，方向与绳垂直．小球相互碰撞时无机械能损失，轻绳不可伸长．求：
如图所示，三个质量均为m的小木块在三个质量均为M、倾角均为α的固定锲块上下滑，它们与锲块间的动摩擦因数各不相同，致使第一小木块加速下滑，第二小木块匀速下滑，第三小木块以初速υ0减速下滑．则在下滑过程中，锲块对地面的压力N1、N2、N3之间的关系为（ ）