题目内容
 如图所示,三个质量均为m的弹性小球用两根长均为L的轻绳连成一条直线而静止在光滑水平面上.现给中间的小球B一个水平初速度v0,方向与绳垂直.小球相互碰撞时无机械能损失,轻绳不可伸长.求:
如图所示,三个质量均为m的弹性小球用两根长均为L的轻绳连成一条直线而静止在光滑水平面上.现给中间的小球B一个水平初速度v0,方向与绳垂直.小球相互碰撞时无机械能损失,轻绳不可伸长.求:(1)当小球A、C第一次相碰时,小球B的速度.
(2)当三个小球再次处在同一直线上时,小球B的速度.
(3)运动过程中小球A的最大动能EKA和此时两根绳的夹角θ.
(4)当三个小球处在同一直线上时,绳中的拉力F的大小.
分析:(1)给中间的小球B一个水平初速度后,由于绳子的拉力作用,小球B减速,小球A和C向前加速,由于两绳子不可伸长,当小球A、C第一次相碰时,角度θ为零,故三球此时在沿B球速度方向的分速度相等,根据动量守恒定律可以列式求解;
(2)根据动量守恒定律和机械能守恒定律列式求解即可;
(3)当小球B速度减为零时,小球A和小球C动能最大,根据动量定律守恒定律和机械能守恒定律联立列式求解;
(4)当三个小球处在同一直线上时,小球B受力平衡,加速度为零,先根据动量定律守恒定律和机械能守恒定律联立列式求解出各个球的速度,再以B球为参考系,根据向心力公式列式求解.
(2)根据动量守恒定律和机械能守恒定律列式求解即可;
(3)当小球B速度减为零时,小球A和小球C动能最大,根据动量定律守恒定律和机械能守恒定律联立列式求解;
(4)当三个小球处在同一直线上时,小球B受力平衡,加速度为零,先根据动量定律守恒定律和机械能守恒定律联立列式求解出各个球的速度,再以B球为参考系,根据向心力公式列式求解.
解答: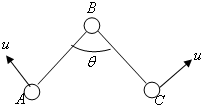 解:(1)设小球A、C第一次相碰时,小球B的速度为vB,考虑到对称性及绳的不可伸长特性,小球A、C沿小球B初速度方向的速度也为vB,由动量守恒定律,得
解:(1)设小球A、C第一次相碰时,小球B的速度为vB,考虑到对称性及绳的不可伸长特性,小球A、C沿小球B初速度方向的速度也为vB,由动量守恒定律,得
mv0=3mvB
由此解得
vB=
v0
即当小球A、C第一次相碰时,小球B的速度为
v0.
(2)当三个小球再次处在同一直线上时,则由动量守恒定律和机械能守恒定律,得
mv0=mvB+2mvA
m
=
m
+2×
m
解得
vB=-
v0
vA=
v0(三球再次处于同一直线)
另一组解为
vB=v0
vA=0(为初始状态,舍去)
所以,三个小球再次处在同一直线上时,小球B的速度为vB=-
v0(负号表明与初速度反向)
(3)当小球A的动能最大时,小球B的速度为零.设此时小球A、C的速度大小为u,两根绳间的夹角为θ(如图),则仍由动量守恒定律和机械能守恒定律,得
mv0=2musin
m
=2×
m
另外,EKA=
mu2
由此可解得,小球A的最大动能为EKA=
mv02,此时两根绳间夹角为θ=90°
即运动过程中小球A的最大动能EKA为
mv02、此时两根绳的夹角θ为90°.
(4)小球A、C均以半径L绕小球B做圆周运动,当三个小球处在同一直线上时,以小球B为参考系(小球B的加速度为0,为惯性参考系),小球A(C)相对于小球B的速度均为
v=|vA-vB|
所以,此时绳中拉力大小为:
F=m
=m
即当三个小球处在同一直线上时,绳中的拉力F的大小为m
.
 解:(1)设小球A、C第一次相碰时,小球B的速度为vB,考虑到对称性及绳的不可伸长特性,小球A、C沿小球B初速度方向的速度也为vB,由动量守恒定律,得
解:(1)设小球A、C第一次相碰时,小球B的速度为vB,考虑到对称性及绳的不可伸长特性,小球A、C沿小球B初速度方向的速度也为vB,由动量守恒定律,得mv0=3mvB
由此解得
vB=
| 1 |
| 3 |
即当小球A、C第一次相碰时,小球B的速度为
| 1 |
| 3 |
(2)当三个小球再次处在同一直线上时,则由动量守恒定律和机械能守恒定律,得
mv0=mvB+2mvA
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 A |
解得
vB=-
| 1 |
| 3 |
vA=
| 2 |
| 3 |
另一组解为
vB=v0
vA=0(为初始状态,舍去)
所以,三个小球再次处在同一直线上时,小球B的速度为vB=-
| 1 |
| 3 |
(3)当小球A的动能最大时,小球B的速度为零.设此时小球A、C的速度大小为u,两根绳间的夹角为θ(如图),则仍由动量守恒定律和机械能守恒定律,得
mv0=2musin
| θ |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| u | 2 |
另外,EKA=
| 1 |
| 2 |
由此可解得,小球A的最大动能为EKA=
| 1 |
| 4 |
即运动过程中小球A的最大动能EKA为
| 1 |
| 4 |
(4)小球A、C均以半径L绕小球B做圆周运动,当三个小球处在同一直线上时,以小球B为参考系(小球B的加速度为0,为惯性参考系),小球A(C)相对于小球B的速度均为
v=|vA-vB|
所以,此时绳中拉力大小为:
F=m
| v2 |
| L |
| ||
| L |
即当三个小球处在同一直线上时,绳中的拉力F的大小为m
| ||
| L |
点评:本题关键要多次结合动量守恒定律和机械能守恒定律列式求解出各个球的速度,计算较为复杂,同时要结合已知的一些临界条件分析.

练习册系列答案
相关题目


 如图所示,三个质量均为m的小木块在三个质量均为M、倾角均为α的固定锲块上下滑,它们与锲块间的动摩擦因数各不相同,致使第一小木块加速下滑,第二小木块匀速下滑,第三小木块以初速υ0减速下滑.则在下滑过程中,锲块对地面的压力N1、N2、N3之间的关系为( )
如图所示,三个质量均为m的小木块在三个质量均为M、倾角均为α的固定锲块上下滑,它们与锲块间的动摩擦因数各不相同,致使第一小木块加速下滑,第二小木块匀速下滑,第三小木块以初速υ0减速下滑.则在下滑过程中,锲块对地面的压力N1、N2、N3之间的关系为( )