Question

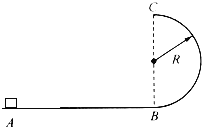
【题目】光滑水平面AB与竖直面内的粗糙半圆形导轨在B点平滑连接，导轨半径为R，一个质量m的小物块在A点以V0= 的速度向B点运动，如图所示，AB=4R，物块沿圆形轨道通过最高点C后做平抛运动，最后恰好落回出发点A．（ g取10m/s2），求：

（1）物块在C点时的速度大小VC

（2）物块在C点处对轨道的压力大小FN

（3）物块从B到C过程克服阻力所做的功．

Answer 1

【答案】（1）（2）3mg，方向竖直向上（3）0.5mgR

【解析】试题分析：(1)物块离开C后做平抛运动，由平抛运动规律可以求出物块到达C点的速度；

(2) 物块做圆周运动，在C点应用牛顿第二定律可以求出回到对物块的作用力，然后由牛顿第三定律求出物块对轨道的作用力；

(3) 由动能定理可以求出克服阻力做功。

解：(1) 物块离开C后做平抛运动，

竖直方向：

水平方向：4R=VCt，

解得：；

(2) 物块在C点做圆周运动，

由牛顿第二定律得：

解得：N=3mg，

由牛顿第三运动定律得，物块对轨道的压力：FN=N=3mg，方向：竖直向上；

（3）对从B到C的过程，由动能定理得：

解得：。

点晴：分析清楚物块的运动过程是正确解题的前提与关键，应用平抛运动规律、牛顿第二定律、动能定理即可正确解题。