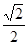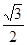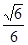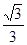题目内容
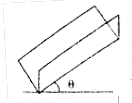
如图所示为一足够长斜面,其倾角为θ=37°,一质量m=5 kg物体,在斜面底部受到一个沿斜面向上的F=50 N的力作用由静止开始运动, 2 s末撤去力F,物体在前2 s内位移为4 m,(sin 37°=0.6,cos 37°=0.8,g=10 m/s2)求:
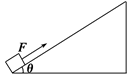
(1)物体与斜面间的动摩擦因数μ;
(2)从静止开始3s内物体的位移和路程.

(1)物体与斜面间的动摩擦因数μ;
(2)从静止开始3s内物体的位移和路程.
(1)0.25 (3)3 m,方向向上。 7 m
(1)前2s内加速度为a1,由题意:S1=1/2a1t12 得a1="2" m/s2 (1分)
根据牛顿第二定律有:F-μmgcos37°-mgsin37°=ma1(2分)
解之得:μ=0.25(1分)
(2)在F被撤消后,物体还要继续向上运动,且是做匀减速运动,当速度为零位移达到最大值。设这过程的加速度为a2,撤消力F时的速度为v,匀减速运动的时间为t2,则有:
mgsin37°+μmgcos37°=ma2 解得:a2=8m/s2 ⑦ (1分)
2s末的速度v= a1t="4" m/s v=a2t2 解得t2=0.5s
匀减速到最高点的位移为S2=1/2a2t22=1m (2分)
之后物体沿斜面向下做匀加速直线运动,
对物体受力分析有: mgsin37°-μmgcos37°=ma3 解得:a3="4" m/s2(1分)
再经过t3="0.5" s 发生位移为S3=1/2a3t32=0.5m(2分)
所以前3.5s位移为S1+S2-S3=4.5m 方向向上(2分) 路程为S1+S2+S3=5.5m(2分)
根据牛顿第二定律有:F-μmgcos37°-mgsin37°=ma1(2分)
解之得:μ=0.25(1分)
(2)在F被撤消后,物体还要继续向上运动,且是做匀减速运动,当速度为零位移达到最大值。设这过程的加速度为a2,撤消力F时的速度为v,匀减速运动的时间为t2,则有:
mgsin37°+μmgcos37°=ma2 解得:a2=8m/s2 ⑦ (1分)
2s末的速度v= a1t="4" m/s v=a2t2 解得t2=0.5s
匀减速到最高点的位移为S2=1/2a2t22=1m (2分)
之后物体沿斜面向下做匀加速直线运动,
对物体受力分析有: mgsin37°-μmgcos37°=ma3 解得:a3="4" m/s2(1分)
再经过t3="0.5" s 发生位移为S3=1/2a3t32=0.5m(2分)
所以前3.5s位移为S1+S2-S3=4.5m 方向向上(2分) 路程为S1+S2+S3=5.5m(2分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

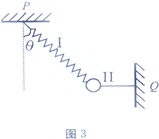
 ,方向水平向左
,方向水平向左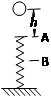
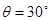 一个横截面为正方形物块,两相邻表面与两槽面接触,且恰好能沿此槽匀速下滑,物块与槽两间动摩擦因数相同,两槽面关于槽的底线对称,则动摩擦因数
一个横截面为正方形物块,两相邻表面与两槽面接触,且恰好能沿此槽匀速下滑,物块与槽两间动摩擦因数相同,两槽面关于槽的底线对称,则动摩擦因数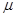 值为( )
值为( )