题目内容
如图所示，一个很长的竖直放置的圆柱形磁铁，产生一个中心辐射的磁场（磁场水平向外），其大小为B=
（其中r为辐射半径），设一个与磁铁同轴的圆形铝环，半径为R（大于圆柱形磁铁的半径），而弯成铝环的铝丝的横截面积为S，圆环通过磁场由静止开始下落，下落过程中圆环平面始终水平，已知铝丝的电阻率为ρ，密度为ρ0，试求： 
（1）圆环下落的速度为v时的电功率；
（2）圆环下落的最终速度；
（3）当下落高度h时速度最大，从开始下落到此时圆环消耗的电能.
(1)
(2) (3)2πρ0RS［gh-
］2
解析:（1）铝环的电阻R电=ρ
=ρ
，当环的速度为v时，它所产生的电动势E=BLv=
·2πRv=2πkv，
故电功率P=
（2）当圆环的加速度为零时，有最大速度.
则FA=BIL=
=
而mg=BIL，解之vm=
.
（3）由能量守恒定律得
Q=mgh-
mvm2=2πρ0RS［gh-
（
）2］
练习册系列答案
应用题作业本系列答案
相关题目
如图所示，一个很长的竖直放置的圆柱形磁铁，在其外部产生一个中心辐射的磁场（磁场水平向外），其大小为B=
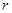(其中r为辐射半径――考察点到圆柱形磁铁中心轴线的距离，k为常数)，设一个与磁铁同轴的圆形铝环，半径为R(大于圆柱形磁铁的半径)，制成铝环的铝丝其横截面积为S，铝环由静止下落通过磁场，下落过程中铝环平面始终水平，已知铝丝电阻率为
，密度为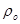
，当地重力加速度为g，试求：
（1）铝环下落的速度为v时铝环的感应电动势是多大？
是多大？
（其中r为辐射半径），设一个与磁铁同轴的圆形铝环，半径为R （大于圆柱形磁铁的半径），而弯成铝环的铝丝其横截面积为S，铝环由静止开始下落，下落过程中铝环平面始终水平，已知铝丝电阻率为ρ，密度为ρ0，试求：
（其中
为辐射半径——考察点到圆柱形磁铁中心轴线的距离，
为常数），设一个与磁铁同轴的圆形铝环，半径为R（大于圆柱形磁铁的半径），制成铝环的铝丝其横截面积为S，铝环由静止下落通过磁场，下落过程中铝环平面始终水平，已知铝丝电阻率为
，密度为
，当地重力加速度为g，试求：
是多大？
（其中
为辐射半径——考察点到圆柱形磁铁中心轴线的距离，
为常数），设一个与磁铁同轴的圆形铝环，半径为R（大于圆柱形磁铁的半径），制成铝环的铝丝其横截面积为S，铝环由静止下落通过磁场，下落过程中铝环平面始终水平，已知铝丝电阻率为
，密度为
，当地重力加速度为g，试求：
是多大？