题目内容
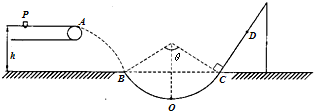
(2011?徐州模拟)质量为m=1kg的小物块轻轻放在水平匀速运动的传送带上的P点,随传送带运动到A点后水平抛出,小物块恰好无碰撞的沿圆弧切线从B点进入竖直光滑圆孤轨道下滑.B、C为圆弧的两端点,其连线水平,斜面与圆弧轨道在C点相切连接(小物块经过C点时机械能损失不计).已知圆弧半径R=1.0m,圆弧对应圆心角θ=106°,轨道最低点为O,A点距水平面的高度h=0.8m.设小物块首次经过C点时为零时刻,在t=0.8s时刻小物块经过D点,小物块与斜面间的滑动摩擦因数为μ1=
.(g=10m/s2,sin37°=0.6,cos37°=0.8)试求:
(1)小物块离开A点的水平初速度vA大小;
(2)小物块经过O点时对轨道的压力;
(3)斜面上CD间的距离.
| 1 | 3 |
(1)小物块离开A点的水平初速度vA大小;
(2)小物块经过O点时对轨道的压力;
(3)斜面上CD间的距离.

分析:(1)小球离开A点做平抛运动,根据竖直方向做自由落体运动,求出竖直方向上的分速度,根据速度与水平方向上的夹角,求出小物块离开A点的水平初速度vA大小.
(2)根据平行四边形定则求出B点的速度,再根据动能定理求出O点的速度,最后根据牛顿第二定律求出支持力的大小,从而由牛顿第三定律求出小物块对O点时的压力.
(3)根据牛顿第二定律求出物块上滑的加速度大小,求出物块上滑到最高点的时间,再根据牛顿第二定律求出物块下滑的加速度,根据运动学公式求出下滑的位移,从而得出斜面上CD间的距离.
(2)根据平行四边形定则求出B点的速度,再根据动能定理求出O点的速度,最后根据牛顿第二定律求出支持力的大小,从而由牛顿第三定律求出小物块对O点时的压力.
(3)根据牛顿第二定律求出物块上滑的加速度大小,求出物块上滑到最高点的时间,再根据牛顿第二定律求出物块下滑的加速度,根据运动学公式求出下滑的位移,从而得出斜面上CD间的距离.
解答:解:(1)对小物块,由A到B有
=2gh
在B点tan
=
所以vA=3m/s
(2)对小物块,由B到O有mgR(1-sin37°)=
m
-
m
vB=
=
m/s=5m/s
在O点 N-mg=m
所以 N=43N
由牛顿第三定律知对轨道的压力为 N'=43N
(3)物块沿斜面上滑:mgsin53°+μ1mgcos53°=ma1
a1=10m/s2
物块沿斜面下滑:mgsin53°-μ1mgcos53°=ma2
a2=6 m/s2
由机械能守恒知vC=vB=5m/s
小物块由C上升到最高点历时t1=
=0.5s
小物块由最高点回到D点历时t2=0.8-0.5=0.3s
故SCD=
t1-
a2
=0.98 m
答:(1)小物块离开A点的水平初速度vA大小为3m/s.
(2)小物块经过O点时对轨道的压力为43N.
(3)斜面上CD间的距离为0.98m.
| v | 2 y |
在B点tan
| θ |
| 2 |
| vy |
| vA |
所以vA=3m/s
(2)对小物块,由B到O有mgR(1-sin37°)=
| 1 |
| 2 |
| v | 2 o |
| 1 |
| 2 |
| v | 2 B |
vB=
|
| 32+42 |
在O点 N-mg=m
| ||
| R |
所以 N=43N
由牛顿第三定律知对轨道的压力为 N'=43N
(3)物块沿斜面上滑:mgsin53°+μ1mgcos53°=ma1
a1=10m/s2
物块沿斜面下滑:mgsin53°-μ1mgcos53°=ma2
a2=6 m/s2
由机械能守恒知vC=vB=5m/s
小物块由C上升到最高点历时t1=
| vC |
| a1 |
小物块由最高点回到D点历时t2=0.8-0.5=0.3s
故SCD=
| vC |
| 2 |
| 1 |
| 2 |
| t | 2 2 |
答:(1)小物块离开A点的水平初速度vA大小为3m/s.
(2)小物块经过O点时对轨道的压力为43N.
(3)斜面上CD间的距离为0.98m.
点评:本题是多过程问题,综合运用了动能定理、牛顿第二定律,关键理清运动过程,选择合适的规律进行求解.

练习册系列答案
相关题目
 (2011?徐州模拟)如图所示,一根轻弹簧上端固定在O点,下端拴一个钢球P,球处于静止状态.现对球施加一个方向向右的外力F,使球缓慢偏移,在移动中的每一个时刻,都可以认为钢球处于平衡状态.若外力F的方向始终水平,移动中弹簧与竖直方向的夹角θ<90°,且弹簧的伸长量不超过其弹性限度,则下图给出的弹簧伸长量x与cosθ的函数关系图象中,最接近的是( )
(2011?徐州模拟)如图所示,一根轻弹簧上端固定在O点,下端拴一个钢球P,球处于静止状态.现对球施加一个方向向右的外力F,使球缓慢偏移,在移动中的每一个时刻,都可以认为钢球处于平衡状态.若外力F的方向始终水平,移动中弹簧与竖直方向的夹角θ<90°,且弹簧的伸长量不超过其弹性限度,则下图给出的弹簧伸长量x与cosθ的函数关系图象中,最接近的是( ) (2011?徐州模拟)质量为m的物体从地面上方H高产无初速释放,落在地面后出现一个深度为h的坑,如图所示,在此过程中( )
(2011?徐州模拟)质量为m的物体从地面上方H高产无初速释放,落在地面后出现一个深度为h的坑,如图所示,在此过程中( ) (2011?徐州模拟)如图所示为一质点运动的位移-时间图象,曲线为一段圆弧,则下列说法中正确的是( )
(2011?徐州模拟)如图所示为一质点运动的位移-时间图象,曲线为一段圆弧,则下列说法中正确的是( ) (2011?徐州模拟)如图所示,空间的虚线框内有匀强电场,AA′、BB′、CC′是该电场的三个等势面,相邻等势面间的距离均为0.5cm,其中BB'为零势能面.一个质量为m,带电量为+q的粒子沿AA′方向以初动能Ek自图中的P点进入电场,刚好从C′点离开电场.已知PA′=2cm.粒子的重力忽略不计.下列说法中正确的是( )
(2011?徐州模拟)如图所示,空间的虚线框内有匀强电场,AA′、BB′、CC′是该电场的三个等势面,相邻等势面间的距离均为0.5cm,其中BB'为零势能面.一个质量为m,带电量为+q的粒子沿AA′方向以初动能Ek自图中的P点进入电场,刚好从C′点离开电场.已知PA′=2cm.粒子的重力忽略不计.下列说法中正确的是( ) (2011?徐州模拟)如图所示,水平放置的平行板电容器,原来两板不带电,上极板接地,它的极板长L=0.1m,两板间距离d=0.4cm,有一束相同微粒组成的带电粒子流以相同的初速度从两板中央平行于极板射入,由于重力作用微粒能落到下板上,到达极板后电荷全部传给极板.已知微粒质量m=2.0×10-6kg,电量q=1.0×10-8C,电容器电容C=1.0×10-6F,取g=10m/s2.试求:
(2011?徐州模拟)如图所示,水平放置的平行板电容器,原来两板不带电,上极板接地,它的极板长L=0.1m,两板间距离d=0.4cm,有一束相同微粒组成的带电粒子流以相同的初速度从两板中央平行于极板射入,由于重力作用微粒能落到下板上,到达极板后电荷全部传给极板.已知微粒质量m=2.0×10-6kg,电量q=1.0×10-8C,电容器电容C=1.0×10-6F,取g=10m/s2.试求: