题目内容
【题目】如图,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动,星球A和B两者中心之间的距离为L,已知A、B的中心和O三点始终共线,A和B分别在O的两侧,引力常数为G。
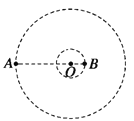
(1)求两星球做圆周运动的周期;
(2)在地月系统中,若忽略其他星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行的周期为![]() 。但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得运行周期记为
。但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得运行周期记为![]() 。已知地球和月球的质量分别为
。已知地球和月球的质量分别为![]() 和
和![]() 。求
。求![]() 与
与![]() 两者平方之比(结果保留三位小数)。
两者平方之比(结果保留三位小数)。
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)A和B绕O做匀速圆周运动,它们之间的万有引力提供向心力,则A和B的向心力大小相等,且A和B和O始终共线,说明A和B有相同的角速度和周期,因此有:![]()
联立解得:![]()
对A根据牛顿第二定律和万有引力定律得:![]()
化简得:![]()
(2)将地月看成双星,由(1)得![]()
将月球看作绕地心做圆周运动,根据牛顿第二定律和万有引力定律得:![]()
化简得:![]()
所以两种周期的平方比值为:![]()

练习册系列答案
相关题目
【题目】图为验证机械能守恒定律的实验装置示意图,现有的器材为:带铁夹的铁架台、电磁打点计时器、纸带、带铁夹的重锤、天平。回答下列问题
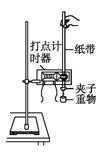
(1)为完成此实验,除了所给的器材,还需要的器材有___________(填入正确选项前的字母)
A.米尺 |
B.秒表 |
C.0~12V的直流电源 |
D.0~12V的交流电源 |
(2)实验中误差产生的原因有_________。(写出两个原因)