题目内容
9.一简谐横波沿水平绳向右传播,波速为v,周期为T,振幅为A.绳上两质点M、N的平衡位置相距$\frac{3}{4}$波长,N位于M右方.设向上为正,在t=0时M位移为+$\frac{A}{2}$,且向上运动;经时间t(t<T),M位移仍为+$\frac{A}{2}$,但向下运动,则( )| A. | 在t时刻,N恰好在波谷位置 | B. | 在t时刻,N位移为负,速度向上 | ||
| C. | 在t时刻,N位移为负,速度向下 | D. | 在2t时刻,N位移为-$\frac{A}{2}$,速度向下 |
分析 在t=0时M位移为+$\frac{A}{2}$,且向上运动;经时间t(t<T),M位移仍为+$\frac{A}{2}$,但向下运动,由此写出M点的振动方程,然后结合M、N的平衡位置相距$\frac{3}{4}$波长,N位于M右方写出N点的振动方程,即可判断出t时刻N点的位置以及振动的方向.
解答 解:A、B、C、由题,在t=0时M位移为+$\frac{A}{2}$,且向上运动,则M点的振动方程为:yM=Asin(ωt+φ0),将在t=0时M位移为+$\frac{A}{2}$代入方程得:
$\frac{A}{2}=A•sin(\frac{2π}{T}•t+{φ}_{0})$
所以:${φ}_{0}=\frac{1}{6}π$
经时间t(t<T),M位移仍为+$\frac{A}{2}$,但向下运动,代入公式得:$t=\frac{1}{3}T$
两质点M、N的平衡位置相距$\frac{3}{4}$波长,N位于M右方,所以N点的振动方程:${y}_{N}=Asin[ω(t-\frac{\frac{3}{4}λ}{v})+{φ}_{0}]$,
代入数据得:yN=$A•sin[\frac{2π}{T}(\frac{1}{3}T-\frac{3}{4}T)+\frac{π}{6}]$=-$\frac{\sqrt{3}}{2}A$,随t的增大,位移的绝对值减小,所以N向下运动.故AB错误,C正确;
D、将2t代入公式,得:${y}_{N}=A•sin[\frac{2π}{T}(\frac{2}{3}T-\frac{3}{4}T)+\frac{π}{6}]=0$,质点恰好经过平衡位置.故D错误.
故选:C
点评 本题是特殊值问题,根据题目提供的条件,写出M点与N点的振动方程,代入数据即可.
由于是特殊值问题,也可以使用特殊值,画出波动的图象,使用平移法解答.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 如图所示,半球形物体A和小球B紧靠着放在一固定斜面上,并处于静止状态,忽略小球B表面的摩擦,用水平力F沿物体A表面将小球B缓慢拉至物体A的最高点C,物体A始终保持静止状态,则下列说法中正确的是( )
如图所示,半球形物体A和小球B紧靠着放在一固定斜面上,并处于静止状态,忽略小球B表面的摩擦,用水平力F沿物体A表面将小球B缓慢拉至物体A的最高点C,物体A始终保持静止状态,则下列说法中正确的是( )| A. | 物体A受到斜面的摩擦力大小始终不变 | |
| B. | 物体A受到4个力的作用 | |
| C. | 小球B对物体A的压力大小始终不变 | |
| D. | 小球B对物体A的压力大小一直增加 |
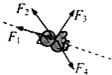
| A. | F1 | B. | F2 | C. | F3 | D. | F4 |

| A. | 光的本质是波 | B. | 光的本质是粒子 | ||
| C. | 光的能量在胶片上分布不均匀 | D. | 光到达胶片上不同位置的概率相同 |
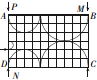 矩形ABCD区域内有方向垂直于纸面向里的匀强磁场,有5个电粒子分别从图中箭头处进入磁场,在磁场中做匀速圆周运动,运动轨迹为ABCD区域内的一段圆弧,粒子的编号、质量、电荷量(q>0)及速度大小如表所示.则从P、M、N处垂直磁场进入的带电粒子分别对应着表格中的粒子编号为( )
矩形ABCD区域内有方向垂直于纸面向里的匀强磁场,有5个电粒子分别从图中箭头处进入磁场,在磁场中做匀速圆周运动,运动轨迹为ABCD区域内的一段圆弧,粒子的编号、质量、电荷量(q>0)及速度大小如表所示.则从P、M、N处垂直磁场进入的带电粒子分别对应着表格中的粒子编号为( ) | 粒子编号 | 粒子质量 | 电荷数 | 速度大小 |
| a | m | 2q | v |
| b | 2m | 2q | 2v |
| c | 3m | -3q | 3v |
| d | 2m | 2q | 3v |
| e | 2m | -q | v |
| A. | d、c、e | B. | b、c、e | C. | e、c、b | D. | b、d、e |
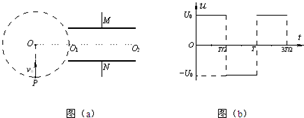 如图(a)所示,在真空中,半径为b的虚线所围的圆形区域内存在匀强磁场,磁场方向与纸面垂直.在磁场右侧有一对平行金属板M和N,两板间距离也为b,板长为2b,两板的中心线O1O2与磁场区域的圆心O在同一直线上,两板左端与O1也在同一直线上.有一电荷量为+q、质量为m的带电粒子,以速率v0从圆周上的P点沿垂直于半径OO1并指向圆心O的方向进入磁场,当从圆周上的O1点飞出磁场时,给M、N板加上如图(b)所示电压u.最后粒子刚好以平行于N板的速度,从N板的边缘飞出.不计平行金属板两端的边缘效应及粒子所受的重力.
如图(a)所示,在真空中,半径为b的虚线所围的圆形区域内存在匀强磁场,磁场方向与纸面垂直.在磁场右侧有一对平行金属板M和N,两板间距离也为b,板长为2b,两板的中心线O1O2与磁场区域的圆心O在同一直线上,两板左端与O1也在同一直线上.有一电荷量为+q、质量为m的带电粒子,以速率v0从圆周上的P点沿垂直于半径OO1并指向圆心O的方向进入磁场,当从圆周上的O1点飞出磁场时,给M、N板加上如图(b)所示电压u.最后粒子刚好以平行于N板的速度,从N板的边缘飞出.不计平行金属板两端的边缘效应及粒子所受的重力. 如图(a),两相距L=0.5m的平行金属导轨固定于水平面上,导轨左端与阻值R=2Ω的电阻连接,导轨间虚线右侧存在垂直导轨平面的匀强磁场.质量m=0.2kg的金属杆垂直置于导轨上,与导轨接触良好,导轨与金属杆的电阻可忽略.杆在水平向右的恒定拉力作用下由静止开始运动,并始终与导轨垂直,其v-t图象如图(b)所示.在15s时撤去拉力,同时使磁场随时间变化,从而保持杆中电流为0.求:
如图(a),两相距L=0.5m的平行金属导轨固定于水平面上,导轨左端与阻值R=2Ω的电阻连接,导轨间虚线右侧存在垂直导轨平面的匀强磁场.质量m=0.2kg的金属杆垂直置于导轨上,与导轨接触良好,导轨与金属杆的电阻可忽略.杆在水平向右的恒定拉力作用下由静止开始运动,并始终与导轨垂直,其v-t图象如图(b)所示.在15s时撤去拉力,同时使磁场随时间变化,从而保持杆中电流为0.求: