Question

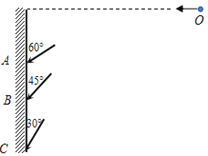
【题目】如图所示，某人从同一位置O以不同的水平速度投出三枚飞镖A、B、C，最后都插在竖直墙壁上，它们与墙面的夹角分别为60°、45°、30°，图中飞镖的取向可认为是击中墙面时的速度方向，不计空气阻力。则下列说法正确的是

A. 三只飞镖做平抛运动的初速度一定满足

B. 三只飞镖击中墙面的速度满足

C. 插在墙上的三只飞镖的反向延长线一定交于同一点

D. 三只飞镖击中墙面的速度一定满足

Answer 1

【答案】ACD

【解析】

飞镖做平抛运动，水平分运动，有：x=v0t，速度与竖直方向夹角的正切值为：，联立解得：v0=，故vAO＞vBO＞vCO，故A正确；飞镖做平抛运动，速度的反向延长线通过水银分位移的中点，而飞镖的指向表示瞬时速度的方向，故插在墙上的三只飞镖的反向延长线一定交于同一点，故C正确；根据平行四边形定则并结合几何关系，有： ，故vA=vC=，vB=，故vA=vC＞vB，故B错误，D正确；故选ACD。