��Ŀ����
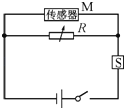
����Ŀ����ͼ����ʾ���ռ����B=0.5T��������ֱ���µ���ǿ�ų���MN��PQ�Ǵ���ͬһˮƽ�����ƽ�еĴֲڳ�ֱ���죬���L=0.2m��R�������ڵ���һ�˵ĵ��裬ab�ǿ���ڵ���������Ϊm=0.1kg�ĵ����������ʱ�̿�ʼ��ͨ��һС�͵綯����ab��ʩ��һ��ǣ����F������ˮƽ����ʹ��Ӿ�ֹ��ʼ�ص����������˶����˹����а�ʼ�ձ����뵼�촹ֱ�ҽӴ����ã�ͼ���ǰ���v��tͼ������OA����ֱ�ߣ�AC�����ߣ�DE������ͼ��Ľ����ߣ�С�͵綯����12sĩ�ﵽ�����P=4.5W���˺ֹ��ʲ��䣮��R�⣬���ಿ�ֵ�������ƣ�g=10m/s2 �� ��
��1��ab��0��12s�ڵļ��ٶȴ�С��
��2��ab�뵼���Ķ�Ħ�������͵���R����ֵ��
��3����t=17sʱ�������ab�ﵽ����ٶȣ���0��17s�ڵ�λ��Ϊ100m����12��17s�ڣ�R�ϲ�����������
���𰸡�
��1���⣺��ͼ��֪12sĩ�����ab���ٶ�Ϊv1=9m/s����0��12s�ڵļ��ٶȴ�СΪ��
a= ![]() =
= ![]() m/s2=0.75m/s2
m/s2=0.75m/s2
��ab��0��12s�ڵļ��ٶȴ�СΪ0.75m/s2��
��2���⣺t1=12sʱ��v1=9m/s��������и�Ӧ�綯��Ϊ��E=BLv1
��Ӧ����Ϊ��I= ![]()
������ܵ��İ�����Ϊ��F1=BIL������F1= ![]()
��ʱ�綯��ǣ����Ϊ��F= ![]()
��ţ�ٵڶ����ɵã� ![]() ��
�� ![]() ����mg=ma
����mg=ma
����ã� ![]() ��
�� ![]() ���̡�0.1��10=0.1��0.75
���̡�0.1��10=0.1��0.75
��ͼ��֪17sĩ�����ab������ٶ�Ϊv2=10m/s����ʱ���ٶ�Ϊ�㣬ͬ���У� ![]() ��
�� ![]() ����mg=0
����mg=0
����ã� ![]() ��
�� ![]() ���̡�0.1��10=0
���̡�0.1��10=0
����=0.2��R=0.4��
��ab�뵼���Ķ�Ħ������Ϊ0.2������R����ֵΪ0.4����
��3���⣺0��12s�ڣ�������ȼ����˶���λ��Ϊ��s1= ![]() t1=
t1= ![]() ��12m=54m
��12m=54m
12��17s�ڣ��������λ��Ϊ��s2=100��54=46m
�������غ�ã�Q=Pt2���� ![]() ��
�� ![]() m
m ![]() ������mgs2=4.5��5��
������mgs2=4.5��5�� ![]() 0.1����102��92����0.2��0.1��10��46=12.35 J
0.1����102��92����0.2��0.1��10��46=12.35 J
��2��17s�ڣ�R�ϲ���������Ϊ12.35J��
����������1��ͼ����0��12s���������ȼ���ֱ���˶����ɸö�ͼ���е�б�ʿ���ü��ٶȣ���2�����ɵ����и�Ÿ���ʱ�ĸ�Ӧ�綯�Ʊ���ʽ����õ綯�ƴ�С����ŷķ���ɿ���ø�Ӧ�����������Ͱ���������ţ�ٵڶ����ɿɵó����ٶȱ���ʽ��ͬ�������17sʱ�ļ��ٶȱ���ʽ������������ö�Ħ������������R����ֵ����3����λ�ƹ�ʽ�����12s�ڵ�λ�ƣ����ɹ��ܹ�ϵ�����R�ϲ�����������
�����㾫����������Ҫ�����˵�Ÿ�Ӧ���·�͵�Ÿ�Ӧ��ͼ������֪ʶ�㣬��Ҫ�����÷����ڵ�Ÿ�Ӧ���ɺ���ζ���ȷ����Ӧ�綯�ƵĴ�С�ͷ�����Ч��·������ȫ��·ŷķ���ɣ���������·���ʣ��繦�ʵȹ�ʽ������⣻��Ÿ�Ӧ������ͼ������ķ�����Ҫץס��ͨ���ı仯�Ƿ���ȣ��Ӷ���֪��Ӧ�綯�ƣ���������С�Ƿ�㶨.����ζ����жϳ���Ӧ�綯�ƣ���������ķ��Ӷ�ȷ�����������Լ��������еķ�Χ������ȷ�����⣮