题目内容
 (2010?淄博一模)(1)雷蒙德?戴维斯因研究来自太阳的电子中微子(νe)而获得了2002年度诺贝尔物理学奖.他探测中微子所用的探测器的主体是一个贮满615t四氯乙烯(C2Cl4)溶液的巨桶.电子中微子可以将一个氯核转变为一个氢核,其核反应方程式为νe+
(2010?淄博一模)(1)雷蒙德?戴维斯因研究来自太阳的电子中微子(νe)而获得了2002年度诺贝尔物理学奖.他探测中微子所用的探测器的主体是一个贮满615t四氯乙烯(C2Cl4)溶液的巨桶.电子中微子可以将一个氯核转变为一个氢核,其核反应方程式为νe+37 17 |
37 18 |
0 -1 |
37 17 |
37 18 |
0 -1 |
0.82
0.82
MeV(结果保留两位有效数字).(2)如图所示,质量为m=1kg的滑块,以v0=5m/s的水平初速度滑上静止在光滑水平面的平板小车,小车足够长,质量M=4kg.求:
①滑块与小车的共同速度v;
②整个运动过程中产生的内能E.
分析:(1)根据题意可知该核反应过程中质量增加,因此需要提供能量,根据质能方程求出反应所需能量,然后根据能量的守恒即可求出中微子的最小能量.
(2)选择正确的研究对象,根据动量守恒定律及能量守恒求解问题.
(2)选择正确的研究对象,根据动量守恒定律及能量守恒求解问题.
解答:解:(1)反应过程需要能量为:E=mc2=(36.95691u+0.00055u-36.95658u)c2
根据l u质量对应的能量为931.5MeV,得:E≈0.82MeV,所以中微子的能量最小为0.82MeV,
故答案为:0.82
(2)①根据动量守恒定律列出等式:
mv0=(m+M)v
解得:v=1m/s
②根据能量守恒知道整个运动过程中产生的内能等于动能的损失.
E=
mv02-
(m+M)v 2
得:E=10J
答:①滑块与小车的共同速度v为1m/s;
②整个运动过程中产生的内能E为10J.
根据l u质量对应的能量为931.5MeV,得:E≈0.82MeV,所以中微子的能量最小为0.82MeV,
故答案为:0.82
(2)①根据动量守恒定律列出等式:
mv0=(m+M)v
解得:v=1m/s
②根据能量守恒知道整个运动过程中产生的内能等于动能的损失.
E=
| 1 |
| 2 |
| 1 |
| 2 |
得:E=10J
答:①滑块与小车的共同速度v为1m/s;
②整个运动过程中产生的内能E为10J.
点评:(1)本题考查了能量守恒在原子物理知识中的应用,要解答这类问题关键是在计算上不要出错.
(2)把动量守恒和能量守恒结合起来列出等式求解是常见的问题.清楚运动过程中能量的转化.
(2)把动量守恒和能量守恒结合起来列出等式求解是常见的问题.清楚运动过程中能量的转化.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
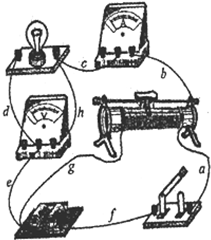
 (2010?淄博一模)如图所示,当滑动变阻器R0的滑动触头P向下滑动时,则下列叙述正确的是( )
(2010?淄博一模)如图所示,当滑动变阻器R0的滑动触头P向下滑动时,则下列叙述正确的是( ) (2010?淄博一模)如图所示,斜面轨道AB与水平面之间的夹角θ=53°,BD为半径R=4m的圆弧形轨道,且B点与D点在同一水平面上,斜面轨道AB与圆弧轨道相切,整个光滑轨道处于竖直平面内.在A点,一质量m=1kg的小球由静止滑下,经过B、C点后从D点飞出去.设以竖直线MDN为分界线,其左边为阻力场区域,右边为真空区域,小球最后落到地面上的S点处时的速度大小vs=8m/s.已知A点距离地面的高度H=10m,B点距离地面的高度h=5m,g取10m/s2,sin53°=0.8,cos53°=0.6,求:
(2010?淄博一模)如图所示,斜面轨道AB与水平面之间的夹角θ=53°,BD为半径R=4m的圆弧形轨道,且B点与D点在同一水平面上,斜面轨道AB与圆弧轨道相切,整个光滑轨道处于竖直平面内.在A点,一质量m=1kg的小球由静止滑下,经过B、C点后从D点飞出去.设以竖直线MDN为分界线,其左边为阻力场区域,右边为真空区域,小球最后落到地面上的S点处时的速度大小vs=8m/s.已知A点距离地面的高度H=10m,B点距离地面的高度h=5m,g取10m/s2,sin53°=0.8,cos53°=0.6,求: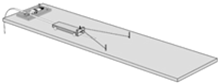



 mv2
mv2