题目内容
直立轻弹簧的下端与水平地面上质量为M=0.20kg的甲木块与连接,轻弹簧上端静止于A点(如图甲),再将质量也为M=0.20kg乙木块与弹簧的上端连接,当甲、乙及弹簧均处于静止状态时,弹簧上端位于B点(如图乙).现向下压乙,当弹簧上端下降到C点时将弹簧锁定,这时C、A两点间的距离为△l=6.0cm.一个质量为m=0.10kg的小球丙从距离乙正上方h=0.45m处自由落下(如图丙),当丙与乙刚接触时,弹簧立即被解除锁定,丙与乙发生弹性碰撞(碰撞时间极短,丙、乙间的作用力远大于重力和弹簧弹力),碰撞后立即取走小球丙.当甲第一次刚离开地面时乙的速度为v=2.0m/s.求:
(1)碰撞刚结束的瞬间,丙球、乙木块的速度v1、v2的大小和方向;
(2)放上乙物体后,平衡时弹簧上端B点(图2中)到A点的距离x1;
(3)从弹簧被解除锁定至甲第一次刚离开地面时,弹簧弹性势能的改变量△EP.(g=10m/s2)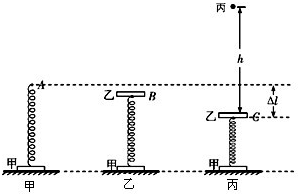
(1)碰撞刚结束的瞬间,丙球、乙木块的速度v1、v2的大小和方向;
(2)放上乙物体后,平衡时弹簧上端B点(图2中)到A点的距离x1;
(3)从弹簧被解除锁定至甲第一次刚离开地面时,弹簧弹性势能的改变量△EP.(g=10m/s2)

(1)规定竖直向下为正方向,设丙自由下落h时速度为v0,根据自由落体运动规律有:
v0=
=3.0m/s
解除锁定后,乙与丙发生弹性碰撞,设碰后乙、丙的速度分别为v2、v1,
由动量守恒mv0=Mv2+mv1
根据机械能守恒
m
=
M
+
m
解得v2=2.0m/s,v1=-1.0m/s
所以v1=1m/s,竖直向上;v2=2m/s,竖直向下.
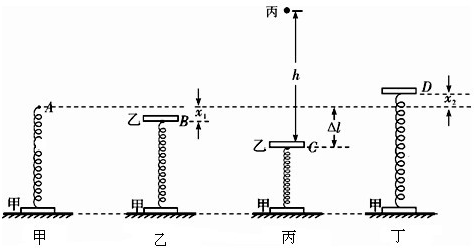
(2)碰后,乙立即以2m/s的速度从C点向下运动,从此时起直到甲第一次刚离开地面前,乙在自身重力和弹簧弹力的共同作用下以B点为平衡位置做简谐运动.
当乙第一次回到平衡位置B时,弹簧相对原长的压缩量(图乙)
x1=
当甲第一次刚离开地面时,弹簧相对原长的伸长量(图丙)
x2=
由于甲第一次刚离开地面时乙的速度为v=2.0m/s,v和v2等大反向,
所以根据简谐振动的对称性可知
x1+x2=△l-x1
故x1=x2=2.0cm.
(3)从碰撞结束至甲第一次刚离开地面时,对于乙和弹簧组成的系统,动能变化量为
△EK=
Mv2-
M
=0
根据功能关系,系统重力势能的增加量△E重等于弹性势能的减少量△E弹
即:△E弹=△E重
而重力势能的增加量为:
△E重=Mg(x2+△l)
所以弹簧弹性势能的减少量为:△E弹=Mg(x2+△l)=0.16J
答:(1)碰撞刚结束的瞬间,丙球的速度为1m/s,方向竖直向上,乙木块的速度为2m/s,方向竖直向下.
(2)放上乙物体后,平衡时弹簧上端B点(图2中)到A点的距离x1为2.0cm.
(3)从弹簧被解除锁定至甲第一次刚离开地面时,弹簧弹性势能的改变量△EP为0.16J.
v0=
| 2gh |
解除锁定后,乙与丙发生弹性碰撞,设碰后乙、丙的速度分别为v2、v1,
由动量守恒mv0=Mv2+mv1
根据机械能守恒
| 1 |
| 2 |
| v | 20 |
| 1 |
| 2 |
| v | 22 |
| 1 |
| 2 |
| v | 21 |
解得v2=2.0m/s,v1=-1.0m/s
所以v1=1m/s,竖直向上;v2=2m/s,竖直向下.

(2)碰后,乙立即以2m/s的速度从C点向下运动,从此时起直到甲第一次刚离开地面前,乙在自身重力和弹簧弹力的共同作用下以B点为平衡位置做简谐运动.
当乙第一次回到平衡位置B时,弹簧相对原长的压缩量(图乙)
x1=
| Mg |
| k |
当甲第一次刚离开地面时,弹簧相对原长的伸长量(图丙)
x2=
| Mg |
| k |
由于甲第一次刚离开地面时乙的速度为v=2.0m/s,v和v2等大反向,
所以根据简谐振动的对称性可知
x1+x2=△l-x1
故x1=x2=2.0cm.
(3)从碰撞结束至甲第一次刚离开地面时,对于乙和弹簧组成的系统,动能变化量为
△EK=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2乙 |
根据功能关系,系统重力势能的增加量△E重等于弹性势能的减少量△E弹
即:△E弹=△E重
而重力势能的增加量为:
△E重=Mg(x2+△l)
所以弹簧弹性势能的减少量为:△E弹=Mg(x2+△l)=0.16J
答:(1)碰撞刚结束的瞬间,丙球的速度为1m/s,方向竖直向上,乙木块的速度为2m/s,方向竖直向下.
(2)放上乙物体后,平衡时弹簧上端B点(图2中)到A点的距离x1为2.0cm.
(3)从弹簧被解除锁定至甲第一次刚离开地面时,弹簧弹性势能的改变量△EP为0.16J.

练习册系列答案
相关题目

 直立轻弹簧的下端与水平地面上质量为M=0.20kg的甲木块与连接,轻弹簧上端静止于A点(如图甲),再将质量也为M=0.20kg乙木块与弹簧的上端连接,当甲、乙及弹簧均处于静止状态时,弹簧上端位于B点(如图乙).现向下压乙,当弹簧上端下降到C点时将弹簧锁定,这时C、A两点间的距离为△l=6.0cm.一个质量为m=0.10kg的小球丙从距离乙正上方h=0.45m处自由落下(如图丙),当丙与乙刚接触时,弹簧立即被解除锁定,丙与乙发生弹性碰撞(碰撞时间极短,丙、乙间的作用力远大于重力和弹簧弹力),碰撞后立即取走小球丙.当甲第一次刚离开地面时乙的速度为v=2.0m/s.求:
直立轻弹簧的下端与水平地面上质量为M=0.20kg的甲木块与连接,轻弹簧上端静止于A点(如图甲),再将质量也为M=0.20kg乙木块与弹簧的上端连接,当甲、乙及弹簧均处于静止状态时,弹簧上端位于B点(如图乙).现向下压乙,当弹簧上端下降到C点时将弹簧锁定,这时C、A两点间的距离为△l=6.0cm.一个质量为m=0.10kg的小球丙从距离乙正上方h=0.45m处自由落下(如图丙),当丙与乙刚接触时,弹簧立即被解除锁定,丙与乙发生弹性碰撞(碰撞时间极短,丙、乙间的作用力远大于重力和弹簧弹力),碰撞后立即取走小球丙.当甲第一次刚离开地面时乙的速度为v=2.0m/s.求:
 如图所示,直立轻弹簧的下端与水平地面上质量为2m的甲木块连接,上端与质量为m的乙木块连接,当甲、乙木块及弹簧均处于静止状态时,弹簧被压缩了h,现将一橡皮泥制成的质量为2m的小球从乙木块正上方H处自由落下,与乙木块碰后粘在一起,当乙木块与橡皮泥小球一起运动到最高点时,甲木块恰要离开地面。现将橡皮泥小球换为等质量的弹性小球,仍从乙木块正上方H处自由落下,当弹性小球与乙木块碰后迅速将弹性小球拿走,求当甲木块刚要离开地面时,乙木块的速度大小。(小球大小不计,与乙木块碰撞时间很短,整个过程弹簧均处在弹性限度内,重力加速度为g)
如图所示,直立轻弹簧的下端与水平地面上质量为2m的甲木块连接,上端与质量为m的乙木块连接,当甲、乙木块及弹簧均处于静止状态时,弹簧被压缩了h,现将一橡皮泥制成的质量为2m的小球从乙木块正上方H处自由落下,与乙木块碰后粘在一起,当乙木块与橡皮泥小球一起运动到最高点时,甲木块恰要离开地面。现将橡皮泥小球换为等质量的弹性小球,仍从乙木块正上方H处自由落下,当弹性小球与乙木块碰后迅速将弹性小球拿走,求当甲木块刚要离开地面时,乙木块的速度大小。(小球大小不计,与乙木块碰撞时间很短,整个过程弹簧均处在弹性限度内,重力加速度为g)