Question

【题目】现代科学仪器常利用电场、磁场控制带电粒子的运动，某装置可用于气体中某些有害离子的收集，如图甲所示，Ⅰ区为加速区，Ⅱ区为离子收集区，其原理是通过板间的电场或磁场使离子偏转并吸附到极板上，达到收集的目的．已知金属极板CE、DF长均为d，间距也为d，AB、CD间的电势差为U，假设质量为m、电荷量为q的大量正离子在AB极均匀分布．离子由静止开始加速进入收集Ⅱ区域，Ⅱ区域板间有匀强电场和垂直于纸面向里的匀强磁场，离子恰好沿直线通过Ⅱ区域；且只撤去电场时，恰好无离子从Ⅱ区域间射出，收集效率(打在极板上的离子占离子总数的百分比)为100%，(不考虑离子间的相互作用力、重力和极板边缘效应)．

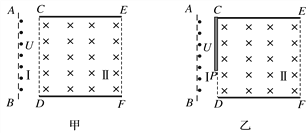
(1)求离子到达Ⅱ区域时的速度大小；

(2)求Ⅱ区域磁感应强度B的大小；

(3)若撤去Ⅱ区域磁场，只保留原来的电场，则装置的收集效率是多少？

(4)现撤去Ⅱ区域的电场，保留磁场但磁感应强度大小可调．假设AB极上有两种正离子，质量分别为m1、m2，且m1≤4m2，电荷量均为q1.现将两种离子完全分离，同时收集更多的离子，需在CD边上放置一探测板CP(离子必须打在探测板上)，如图乙所示．在探测板下端留有狭缝PD，离子只能通过狭缝进入磁场进行分离，试求狭缝PD宽度的最大值。

Answer 1

【答案】（1） （2） （3）50%（4）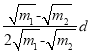

【解析】 (1)离子在Ⅰ区域以初速度0开始加速，由动能定理：

qU＝mv2

可得v＝.

(2)Ⅱ区域只撤去电场时，沿DF极板进入的离子恰好不从极板射出，确定圆心，离子在磁场中的半径r＝d，如图所示．

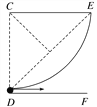
磁场中洛伦兹力提供向心力：

qvB＝m

B＝.

(3)电场、磁场同时存在时，离子直线通过Ⅱ区域，满足：

qE＝qvB

撤去磁场以后离子在电场力作用下做类平抛运动，假设进入Ⅱ区域时距离DF极板为y的离子恰好离开电场：

由平抛运动规律：y＝at2

d＝vt

qE＝ma

解得：y＝0.5d

当y>0.5d时，离子运动到Ⅱ区域的右边界时仍位于DF极板的上方，因此离子会射出Ⅱ区域，即进入Ⅱ区域时到DF极板的距离为0.5d到d的离子会射出电场，则打在极板上的离子数占总数的百分比为

×100%＝50%.

(4)设两离子在磁场中做圆周运动的半径为R1和R2，根据洛伦兹力提供向心力得

qvB＝m

代入得：R1＝，R2＝

则半径关系为＝

因为m1≤4m2，则有R1≤2R2，此时狭缝最大值x同时满足(如图所示)

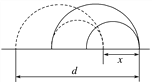
x＝2R1－2R2

d＝2R1＋x

解得：x＝d