题目内容
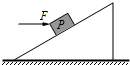 如图所示,位于光滑固定斜面上的小物块 P 受到一水平向右的推力 F 的作用,已知物块 P 沿斜面加速下滑,现保持 F 的方向不变,使其减小,则加速度( )
如图所示,位于光滑固定斜面上的小物块 P 受到一水平向右的推力 F 的作用,已知物块 P 沿斜面加速下滑,现保持 F 的方向不变,使其减小,则加速度( )分析:对物块进行受力分析,物块受重力、支持力、推力,沿斜面加速下滑,知加速度的方向沿斜面向下,根据牛顿第二定律列出方程,根据F的变化,可知加速度的变化.
解答:解:小物块P在推力F的作用下,沿光滑固定斜面加速下滑,设小物块的质量为m,斜面的倾角为θ,分析小物块的受力,并建立小物块的动力学方程,由牛顿第二定律,有:mgsinθ-Fcosθ=ma
∴a=gsinθ-
.当保持F的方向不变,使其减小时,则加速度a一定变大.故B正确,A、C、D错误.
故选B.
∴a=gsinθ-
| Fcosθ |
| m |
故选B.
点评:解决本题的关键熟练运用正交分解,根据牛顿第二定律求出加速度.

练习册系列答案
相关题目
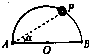 如图所示在光滑绝缘水平面上,电荷量为Q1,Q2两个正点电荷分别固定于A点和B点,两点相距L.在以L为直径的光滑绝缘半圆环也位于水平面上,其上穿着一个带电小球+q(视为质点),在P点平衡,PA与AB的夹角为α,且α<45°.则( )
如图所示在光滑绝缘水平面上,电荷量为Q1,Q2两个正点电荷分别固定于A点和B点,两点相距L.在以L为直径的光滑绝缘半圆环也位于水平面上,其上穿着一个带电小球+q(视为质点),在P点平衡,PA与AB的夹角为α,且α<45°.则( )A、tan2α=
| ||
B、tanα=
| ||
| C、Q1<Q2 | ||
| D、O点的场强方向沿A指向B |
 如图所示,水平轨道PAB与
如图所示,水平轨道PAB与
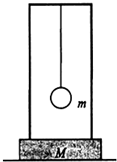 (2012?桂林模拟)如图所示,一木块位于光滑的水平桌面上,木块上固连一支架,木块与支架的总质量为M.一摆球挂于支架上,摆球的质量为m,
(2012?桂林模拟)如图所示,一木块位于光滑的水平桌面上,木块上固连一支架,木块与支架的总质量为M.一摆球挂于支架上,摆球的质量为m, 摆线的质量不计.初始时,整个装置处于静止状态.一质量为m的子弹以大小为v、方向垂直于图面向里的速度射人摆球并立即停留在球内,摆球和子弹便一起开始运动.已知摆线最大的偏转角小于90°,在小球往返运动过程中摆线始终是拉直的,木块未发生转动.
摆线的质量不计.初始时,整个装置处于静止状态.一质量为m的子弹以大小为v、方向垂直于图面向里的速度射人摆球并立即停留在球内,摆球和子弹便一起开始运动.已知摆线最大的偏转角小于90°,在小球往返运动过程中摆线始终是拉直的,木块未发生转动.