题目内容
【题目】如图,一不可伸长的轻绳上端悬挂于O点,下端系一质量m=1.0kg的小球.现将小球拉到A点(保持绳绷直)由静止释放,当它经过B点时绳恰好被拉断,小球平抛后落在水平地面上的C点.地面上的D点与OB在同一竖直线上,已知绳长L=1.0m,B点离地高度H=1.0m,A、B两点的高度差h=0.5m,重力加速度g取10m/s2 , 不计空气影响,求: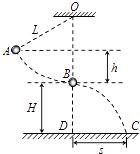
(1)地面上DC两点间的距离s;
(2)轻绳所受的最大拉力大小.
【答案】
(1)解:设小球在B点速度为v,对小球从A到B由动能定理得:
mgh= ![]() mv2①
mv2①
绳子断后,小球做平抛运动,运动时间为t,则有:
H= ![]() ②
②
DC间距离:
s=vt
解得:s= ![]() m≈1.414m
m≈1.414m
答:DC两点间的距离1.414m
(2)解:在B位置,设绳子最大力量为F,由牛顿第二定律得:
F﹣mg= ![]() ④
④
联立①④得:F=2mg=2×1×10N=20N
根据牛顿第三定律,有F'=F,因而轻绳所受的最大拉力为20N.
答:轻绳所受的最大拉力20N
【解析】(1)从A到B由动能定理可得B位置时的速度,之后做平抛运动,由平抛规律求解;(2)在B位置,由牛顿第二定律可求轻绳所受的最大拉力大小.

练习册系列答案
相关题目