��Ŀ����
����Ŀ����ͼ����ʾ����ƽ�н�����AB�������ͼ����ʾ�ĵ�ѹ�������ĵ糡�ɿ�����ǿ�糡�����������糡���峤L=0��8m��������d=0��6m���ڽ������Ҳ���һ�Ÿ�Ӧǿ��B=2��0��10��2T������ֱֽ���������ǿ�ų����ų�����Ϊl1=0��12m���ų��㹻����MNΪһ��ֱ���õ��㹻���ӫ������ӫ������ų��ұ߽�ľ���Ϊl2=0��08m��MN���ų��߽����AB��������OO�䴹ֱ�����д�������������ɽ��������������OO����������糡������֪ÿ�����ӵ��ٶ�v0=4��0��105m/s���Ⱥ�![]() =1��0��108C/kg���������Բ��ƣ�ÿ������ͨ���糡�����ʱ�伫�̣��糡����Ϊ�㶨������
=1��0��108C/kg���������Բ��ƣ�ÿ������ͨ���糡�����ʱ�伫�̣��糡����Ϊ�㶨������
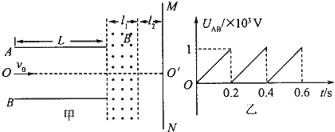
��1����t=0ʱ�̽���糡�����Ӵ�ӫ������ʱƫ��O���ľ��룻
��2��������ǡ���ܴӽ������Ե�뿪�����ʱ�������ϵĵ�ѹ��
��3���������뿪�糡�����ӵ�����ٶȣ���ͨ�������жϸ������ܷ�����Ҳ��ӫ�����ϣ�����ܴ���ӫ�����ϣ�������ںδ���
���𰸡���1��0��10m����2��900V����3��5��105m/s�������Ӳ��ܴ����Ҳ��ӫ��������
��������
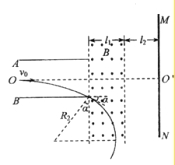
�����������1��t=0ʱ����糡����������ͨ���糡������ų���������Բ���˶������������ṩ��������
��ţ�ٵڶ����ɵã� ![]() ���������ݽ�ã�R1=0��2m��
���������ݽ�ã�R1=0��2m��
�����˶��켣��ͼ��ʾ��
�ɼ���֪ʶ�ɵã� ![]()
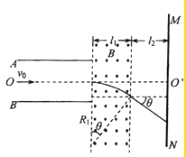
�����ڴų���ƫ�Ƶľ��룺y1=R1��R1cos��
�������ݽ�ã�y1=0��04m
���ӳ��ų���������ֱ���˶���y2=l2tan����
�������ݽ�ã�y2=0��06m��
���Ӵ�ӫ������ʱƫ��O���ľ���Ϊ��y=y1+y2=0��10m
��2����������ѹΪU1ʱ���������ӸպôӼ����Ե����糡��
![]() ��
�� ![]() ��L=v0t��
��L=v0t��
��ã�U1=900V
��3���ɶ��ܶ����ã�![]()
�������ݽ�ã� v1=5��105m/s
�����ڵ糡�е�ƫ�������![]() ��
��
�����ڴų���������Բ���˶������������ṩ��������
��ţ�ٵڶ����ɵã� ![]() ��
��
�������ݽ�ã�R2=0��25m��
R2��R2sin��=0��25��0��25��![]() =0��1m��l1=0��12m
=0��1m��l1=0��12m
�����Ӳ��ܴӴų�ƫ������ӫ�����ϣ�